Constructing the Cheops Pyramid Through Multispiral Ramps

The Cheops Pyramid is the largest Egyptian pyramid and is therefore also known as the Great Pyramid. It was built around 2600 BC and is considered the tomb of the Pharaoh Cheops with the Egyptian name Khufu. The pyramid is the oldest of the Seven Wonders of the Ancient World and the only one to remain largely intact.

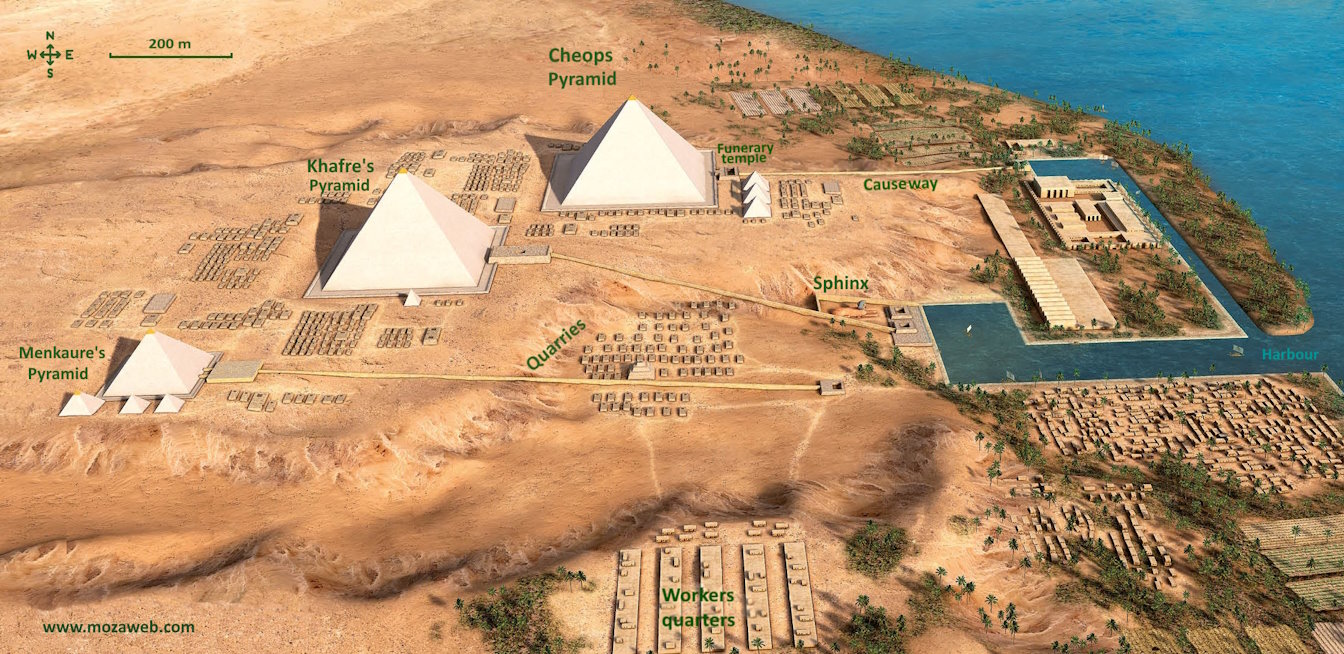
The image from Mozaik Education shows the Pyramids of Giza from 4500 years ago. There is also a 3D representation of this.

The casing out of white limestone made the pyramids appear like diamonds in the sunlight.

Although the Great Pyramid is one of the most impressive structures of mankind, there are almost no documents or archaeological finds that indicate its construction technique.
The pyramid builders belonged to a high guild, which probably kept their knowledge extremely to themselves. They made sure that all notes were destroyed.
According to the two historians Herodotus and Diodorus, the construction time was only 20 years.
How could the Egyptians in the Old Kingdom build this pyramid?
There are many theories about this. However, most of which are completely absurd and none of them can explain the construction completely and satisfactorily. Therefore, this problem is considered as a mystery of mankind.
The solution to the mystery can be expressed briefly:
Spiral ramps and wooden rollers.
At first this may seem sobering, as both elements have been discussed for over 100 years. The combination of efficient transport techniques and the arrangement of the ramp paths leads to a solution. See the sections „Multispiral Model“ and „Tow Team“.
The construction of the pyramid was the largest and most important project for the pharaoh to ensure his reputation in posterity.
This project would never have been started
without a clear and controllable technology.
The construction is consistent with the few archaeological finds and historical evidence. See the „Historical Evidence“ section.
The task of future archaeologists will be to examine the outermost layer of the pyramid for ramp traces. See the „Archaeological Finds“ section.

External Ramp

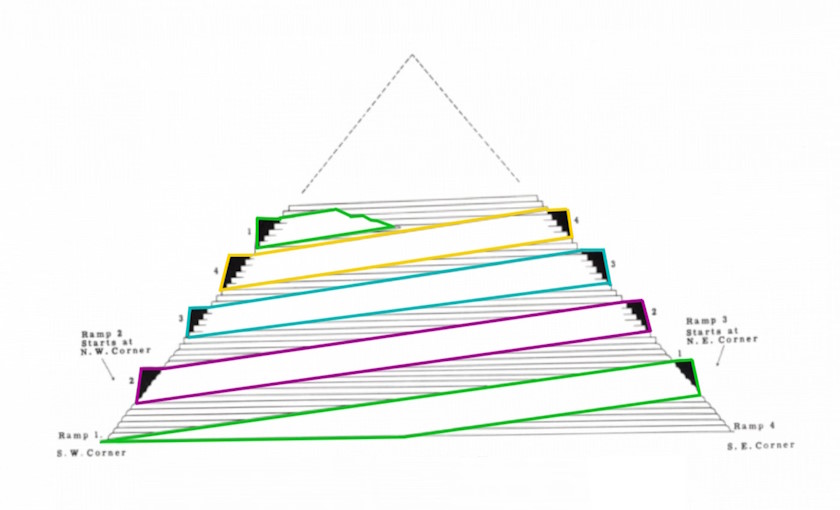
Using an external ramp seems to be the most immediate method. This ramp model was proposed by Ludwig Borchardt in 1928.

With an inclination angle of 6.6 degrees or 11.6 %, the ramp would have a length of 1.2 km and a volume of 135 % relative to the pyramid.

Since the two neighboring pyramids did not exist at that time, the ramp could have looked like demonstarted in the image. This is probably the only way to place an external ramp in this landscape.

It would take more than 10 years to remove this ramp. Therefore, it is impossible to complete this monument within 20 years
If this critical time limit would not exist, then the external ramp would have been considered as a possible solution to the problem for long. Therefore, other possibilities must be considered.
The Sphinx probably already existed at this time and had an animal head that was larger than today’s. Sculptures as hybrid creatures only existed from around 1500 BC.

Seven Misfortunes

In 1799, the Rosetta Stone was found containing Egyptian hieroglyphs and ancient Greek texts. Within just three years, the physicist Thomas Young partially succeeded in deciphering the hieroglyphs, what was completed by Jean-François Champollion.

On the other hand, the mystery surrounding the construction of the Egyptian pyramids has not been solved in the last 200 years. What are the causes for this?

1) The ancient Egyptians left no written documents regarding the construction of the pyramids. This meant that historians had no way of solving the mystery.

2) After the pyramids were completed, the Giza Plateau was considered a representative location. Therefore, it is understandable that all building rubble was cleared away, depriving the archaeologists of their work base. In addition, plenty of mastabas for higher officials were placed next to the pyramids later on, so possible archaeological traces may have been removed.

3) There are some archaeological finds at earlier pyramids. However, these were smaller and different in structure. The construction method did always change. Only the previous construction, the Red Pyramid, was the first real pyramid.

4) The historian Herodotus reported in 450 BC that the pyramids were built by slaves. But he had his information from dubious sources.

Accordingly, his description of the stepped stairs was misinterpreted. This was supplemented by a description of lifting devices.

The picture by Antoine-Yves Goguet from 1758, which was probably recolored, represents the distorted view of history.

Such a block of stone weighs more than 15 tons and cannot possibly be transported in this way by 12 workers. In addition, the wooden beam of the lifting device would not be able to withstand this load.

5) The Museum of Science in Boston developed a model for building the Pyramid of Menkaure in 1950.

The archaeologist Dows Dunham from Harvard University played a key role in this project. He received the gold medal from the Archaeological Institute of America in 1979.

Walter Vose from the Massachusetts Institute of Technology provided practical engineering advice on the project.

The artist Peter Jackson made this lithograph probably based on this project.

In 1956, Dows Dunham made a corresponding publication in the journal Archaeology.

This includes the recolored graphic, which shows how a spiral path starts on each of the 4 sides. That was a tremendous innovation at the time.

This ramp model is briefly mentioned in the books by Georges Goyon and Mark Lehner, it is stated to be interesting but unsuitable.

Ultimately, it is completely inexplicable why this pioneering work has received little attention from experts for 70 years and no one has tried to develop it further.

6) A possible explanation is that spiral ramps were discredited for three reasons and therefore, not considered a serious solution. Firstly, it was impossible to explain how the huge blocks were turned 90 degrees at the corners. Secondly, the spiral ramps were criticized for not having enough transport capacity in the lower and middle areas of the pyramid.

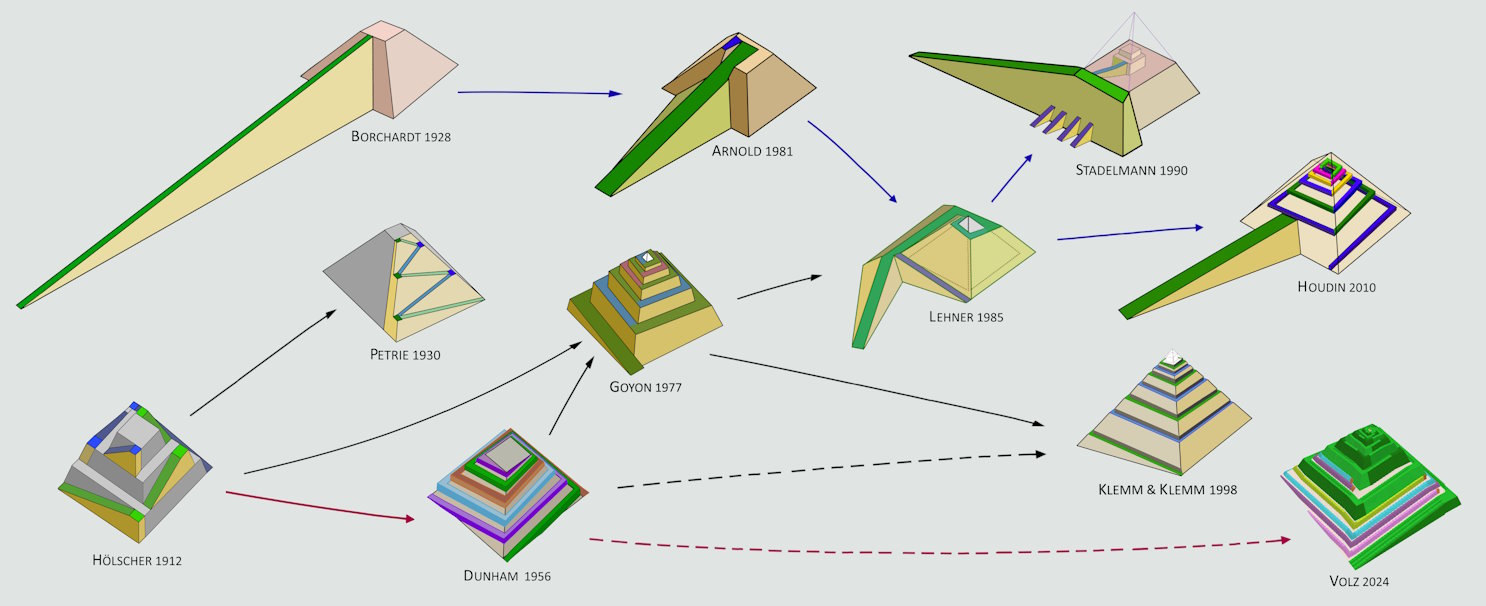
All other models were widely discussed. In particular, the models by Georges Goyon, Mark Lehner and Jean-Pierre Houdin received a lot of attention, although for each model there are several reasons why it is not a solution. One reason they have in common is that in the upper half of the pyramid they use one spiral path with only one transport lane without a separate way back. Thus, the construction time would be more than 30 years.

In the first two models, the outer casing is completely covered by the ramps. Therefore, measurements are hardly possible, which led to a third discredit.

7) Overall, the opinion among archaeologists has emerged that ramps are the most tenable method of lifting the blocks. However, this is an incomplete method that must be supplemented by another device. That’s why so-called combination models have been favored since 1980.

These are suggestions for completing the Four Spiral Model by Dows Dunham:

The huge blocks don’t need to be turned at all, since they only take up a maximum of 2 % of the pyramid’s volume. See the „Huge Blocks“ section. This eliminates the first discredit of the spiral ramps.
In the lower half of the pyramid, some ramps must have a lager width so that there is enough transport capacity. See section „Multispiral Model“. This eliminates the second discredit.
When building on levels, measurements can be done at any time. The precise measurement is carried out in a top-down process when attaching the outer casing. See “Measurements and Precision” section. This eliminates the third discredit.
Some ramps end at different heights since space becomes narrower at the top.
Only one ramp with a width of at least 6 m leads to the top of the pyramid. This allows the pyramidion to be placed on top.
This system of ramps has enough transport capacity in the middle and upper areas of the pyramid. See section „Construction Time“.
The ramp material is made of dried mud-bricks. These are transported using the chain principle. See the „Ramp Construction“ section.
Last but not least, the system needs a reasonable transport method. There may well be historical evidence for the method of sliding sledges on wooden beams, but this is completely unsuitable for the construction of the pyramid. A comparable method using sledges on rollers requires only half the towing team. See “Towing Team” section. In addition, the sliding sledge method requires an enormous number of water carriers and the barefoot workers would constantly slip on the wet Nile mud.

Conclusion:
The adapted model is not a combination model. None of the sublimentary devices are required, which are generally not suitable for mass transport. It is rather an optimization of a dynamic ramp system.
The construction of the Great Pyramid was the most important project in the state. This was always linked to the fight against time. If there had not been a clear and manageable technology, the project would never have been started. See the „Strategy“ section.

The following image shows the evolutionary lines of the ramp models. The dashed lines indicate that the corresponding models were created independently and without knowledge of the previous model by Dows Dunham, since it was almost not mentioned in the literature.

Uniform Pyramid

To better understand the construction of a pyramid, let’s consider a uniform step pyramid with 5 levels. All stones or blocks have the same shape.

The number of blocks is calculated from top to bottom as follows:
B = 1 + 2⋅2 + 3⋅3 + 4⋅4 + 5⋅5
= 1 + 4 + 9 + 16 + 25
= 55

Then the inner step pyramid is decorated with an outer casing. The corner and deco stones of the casing are placed on the steps of the inner pyramid.

There is an additional level with a gold-plated keystone at the very top. This stone is a mini pyramid and is called pyramidion.

The Great Pyramid consists of 210 levels including the Pyramidion. As a uniform pyramid, the Great Pyramid would have 3 million blocks.

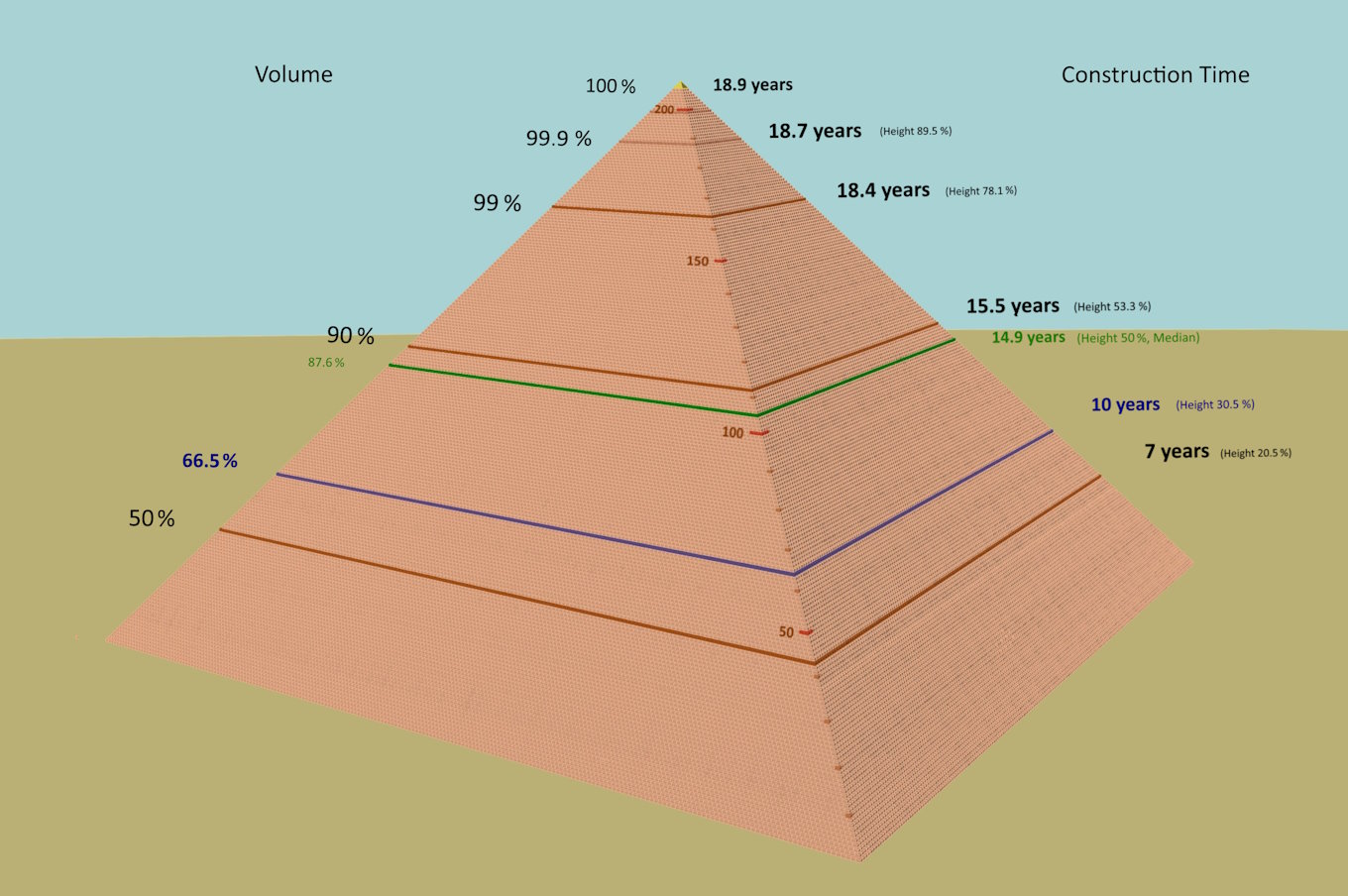
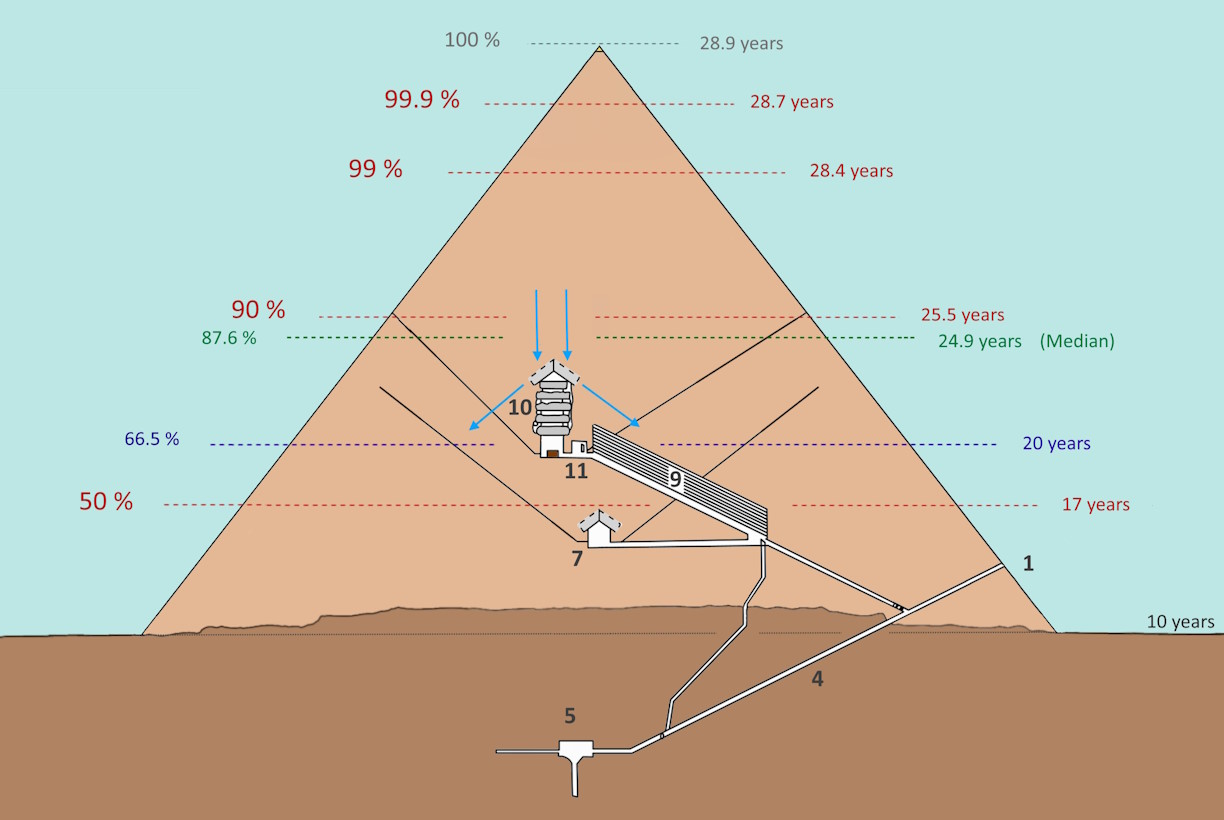
The lowest red line indicates the height at which half or 50 % of the material was installed. This process took 7 years and only a height of 20.5 % was reached at that point.

The blue line shows the height after half of the construction period or after 10 years. Two thirds of the material was installed at that point.

The green line stands for half of the height or the median. This construction phase was reached after three quarters of the construction time or 15 years.

Thus, for many years the Pharaoh saw only a truncated pyramid which did slowly grow.

A uniform block of the Cheops Pyramid is 1.1 m wide, 0.7 m high and weighs 2.3 tons.

The Great Pyramid is by no means uniform. The blocks inside are very irregular.

Using a model of a uniform pyramid, the calculations can be presented more clearly. The uniform block provides a unit of measurement for the amount of material produced and installed.

However, this does neither change the total amount nor the position of the material installed.

Ramp Construction

The ramp paths are directed parallel to the sides of the pyramids. The first element rests completely on the earth’s surface. The next higher element is shifted towards the pyramid by half a block width.

A transport lane is 3 blocks wide, which provides enough space to transport the blocks.

The ramps are built from air-dried mud-bricks. This is an abundant and solid building material

Reed stems, branches and other plant material are installed between the bricks, which are shown in green. This ensures that the ramps hold together, similar to the steel mats in concrete.

The ramps were built using dried mud-bricks, which were transported using the chain principle.

Since a brick weighs around 12 kg, it can be assumed that many workers under the age of 14 were used.

Parallel ramps not only have the advantage that they require less material than perpendicular ramps, but also that the stone blocks can be delivered independently of the construction of the ramps. Two delivery lanes for the blocks are shown in orange.

The image shows a cross section of two ramp paths. In order to better distinguish the individual paths, they are shown in different colors. The natural color would be brown.

The light blue path consists only of a transport lane and is 3 blocks wide. The green path is 9 blocks wide and therefore consists of 3 parallel transport lanes.

The black triangle can be viewed as a stretch of the blue triangle in 2 dimensions by a factor of 3. The area of the black triangle is therefore 9 times the area of the blue triangle.

As a consequence, the green path with 3 transport lanes requires 9 times as much ramp material as the light blue path. Both paths have the same length.

In order for a ramp model to require as little ramp material as possible, it must not consist of one wide path, but rather of several narrow paths.

Multispiral Model

The main green ramp starts from the south side which is close to the quarries. When starting at the bottom, this ramp has 6 transport lanes, after the first turn only 3 lanes.

The main ramp leads to the top of the pyramid. In the upper third of the pyramid, the ramp paths partially rest on the path below.

When transporting a block from the bottom to the top, a distance of 1.8 km is covered and 8 circuits are made. The transport takes 12 hours, which corresponds to almost 2 work shifts.

On the other 3 sides there start 2 ramps with only one transport lane.

These 6 single paths end at different heights. The ends are marked in red.

The entire model consists of 7 spiral paths.

The dark blue ramp ends at the north entrance which is marked in black. This was a restricted access area.

The green main ramp has 6 lanes in the initial phase. After the first turn of the ramp after 5 years, the outer 3 lanes can be dismantled and the ramp material can be reused further up. This is dynamic ramp construction. The boundary line is marked in orange.
The total ramp material has a volume of only 8 % of the volume of the pyramid. This is a huge advantage over the external ramp, which has a volume of 135 %.
The many ramp paths make it possible to create a working platform at almost any location for the later application of the outer casing. See section „Outer Casing“.

Three-Spiral Model

The theory of spiral ramps allows for further variations.

In order to keep the delivery route from the quarries as short as possible, the entire delivery is made via the green main ramp.

In the initial phase, this ramp path has 8 transport lanes. After the first turn, there are 6 lanes and in the upper half of the pyramid there are only 3 lanes.

This model has a certain similarity to the single-spiral model by Georges Goyon.

The purple ramp path is only for the way back. This creates a circular movement of the workers.

The dark blue ramp is only for access to the north entrance. By starting on the northwest side, this area is automatically sealed off.

Due to the wider ramps, this model requires more ramp material. As the pyramid increases in height, the ramp material can be mined from the outside inwards up to the orange line and reused further up, reducing the ramp material from 15 % to 9 %.
When building the inner step pyramid, a lot of ramp material had to be relocated.
When installing the outer casing, a large part of the work platforms must be created. The blocks for the outer casing can only be delivered to one location and then have to be transported further on the work platform.
Blocks weighing 50 tons can be transported on the wide ramp up to half the height of the pyramid.
Wide ramps have less stability.
Ultimately, it is difficult to decide which of the two models has the greater advantage. The three-spiral model has the advantage of being simpler and clearer and probably corresponded better to the habits of the time. A clear decision can only be made archaeologically by examining the remains of ramp material between the stone blocks. See the section „Archaeological Traces“.

Tow Team

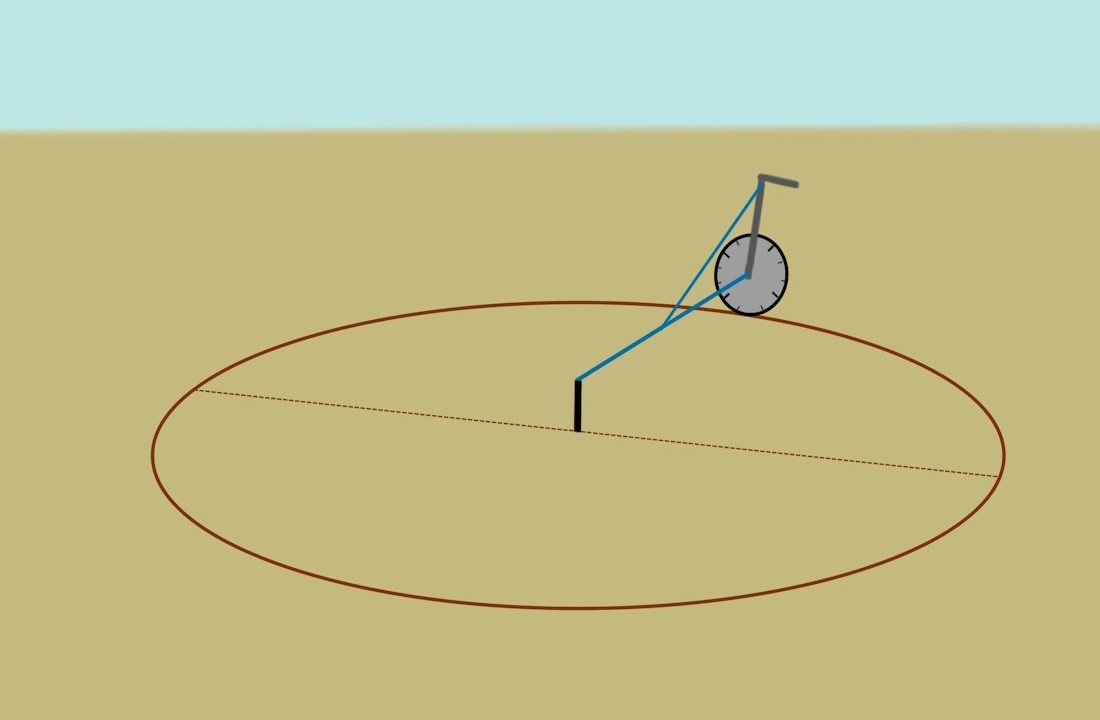
A tow team of 18 workers is required to transport a 2.3 ton block.

At the command of the commander (4), ten workers (5) pull simultaneously for one second with a force of 35 kp. This moves the sledge with the block by 25 cm.

The two workers (6) on the right are enjoying the break.

The two workers (3) with the wooden bares ensure that the rollers remain parallel and do not jam.

After the towing process, the sledge stands for 4 seconds while the tow workers (5) reposition themselves.

The two workers (3) clamp the wooden bars between the rollers, what prevents the sledge from rolling back.

The worker (1) on the far left must always stand behind the sledge and catch the rollers. This prevents the rolls from falling off the pyramid, which is a massive risk of accidents.

The two workers (2) transport the rollers from back to front and reposition them.

Within 5 seconds the team moves 25 cm, which corresponds to a speed of 3 m/min.
The team has a space of movement of 12.1 m. This is marked with the orange lines.
All teams must move at the same speed to avoid jams.
The strain on workers over 6 hours with rotating breaks can be compared to today’s working conditions and corresponds in no way to slave conditions.
The transport method requires that the surfaces of the ramps are kept smooth and stable at all times.

In the literature, there are almost exclusively presented a transport method in which sledges are pulled over wooden beams. The beams are constantly lubricated with Nile mud to reduce friction. See the picture above by Peter Jackson.

The size of the towing team is almost the same as when transporting with wooden rollers. Without the use of wooden beams and Nile mud, the tow team would have to be at least twice as large.

However, water carriers are required in addition when using Nile mud.

The water carriers have to deliver the Nile mud not only at the end of the delivery lane, but for all tow teams along the entire transport lane.
When building the upper half of the pyramid, the paths are longer than 1 km and the number of water carriers increases considerably.
The water carriers require a separate walkway because they are numerous and move at three times the speed of the towing teams. Therefore, the ramps must be wider.
In addition, the workers would have difficulty moving on the slippery transport paths.
By comparison, it can be stated that with this transport technology, the efficiency would fall by 20 % and the construction time would be 24 years.
The greatest possible efficiency was required because the project was a fight against time.

Construction Time

The image shows level 112, where 90 % of the material has been installed.

The pyramidion was transported up to there from level to level. All the huge blocks had been installed by then.

The main green path leads to this level with 3 lanes. There are also the light blue and dark purple paths, each with one lane. So a total of 5 lanes lead to this level.

When subtracting one lane for the way back, there are still 4 lanes left for delivering the blocks.

This level has a width of 210 – 112 = 98 block widths.
Therefore it consists of 98 ⋅ 98 = 9,604 blocks.
There can be 180 blocks delivered per day and per transport lane.
A total of 720 blocks could be delivered with 4 transport lanes per day.
Due to the length of the paths, this would require more than 20,000 workers. Therefore, a maximum of 589 blocks can be produced and delivered per day. This only applied during the 3 months of the Nile flood.
In the remaining 9 months outside of the Nile flood, there were only 10,000 workers. Therefore, only 294 blocks could be delivered per day.
This results in an annual average of 368 blocks per working day.
Therefore, this level has a construction time of 9,604 / 368 = 26.1 working days.
Since there were 300 working days per year, this corresponds to 0.09 years or about one month.
The values for all 210 levels can be determined in this way. By adding the values for all levels results in the construction time of 19.1 years for the inner step pyramid. This is the corresponding table for the construction time.
The outer casing requires only 0.7 % of the material and a construction time of 0.7 years.
The total construction time is therefore 19.8 years.
This model proves that the system of spiral ramps has sufficient transport capacity in the upper range of the pyramid. This is in contradiction to the literature. There are only models used that have only one transport lane in the upper two thirds of the pyramid without a separate way back. In this case the construction period would be at least 30 years.
The transport problem can be completely solved with the described system of ramps. No further technology is necessary. This is contrary to the literature where it is mentioned that ramps require supplementary devices.

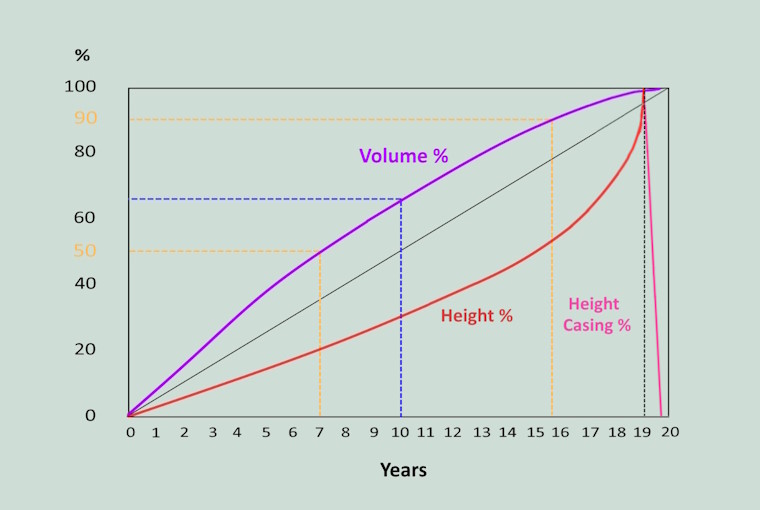
The diagram shows how the volume and height of the pyramid developed within the construction period of 20 years.

The blue dashed line indicates that after 10 years a height of 30 % was reached and the volume of 67 % was built. See the corresponding image in the „Uniform Pyramid“ section.

The black dashed line indicates that the height of 100 % was reached after 19.1 years when the pyramidion was placed.

Then the outer casing was installed from top to bottom in 0.7 years, so that the construction was completed after 19.8 years.

Workforce

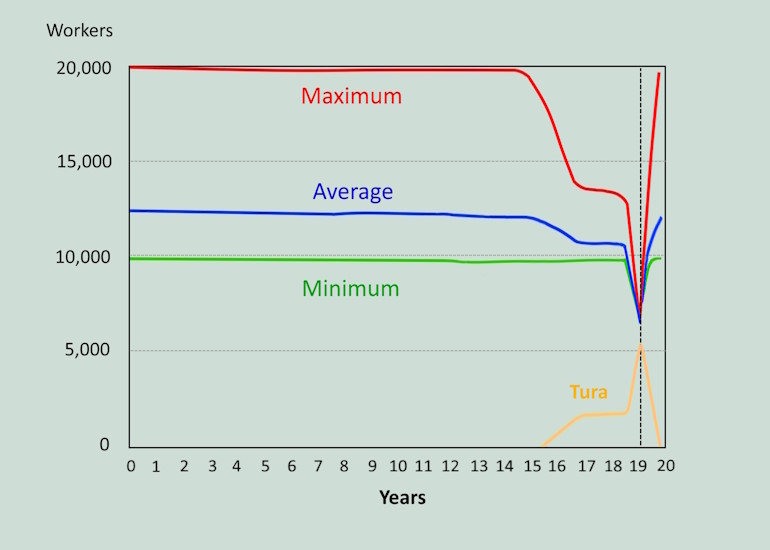
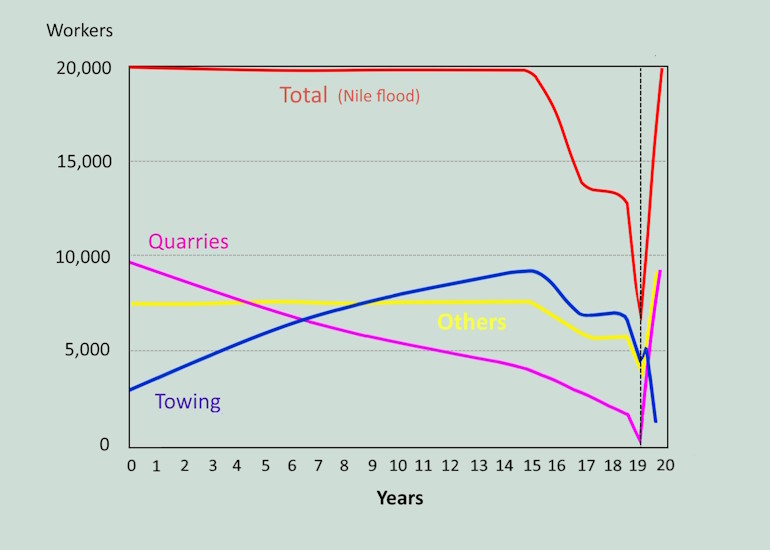
During the Nile flood, around 20,000 workers were employed at the pyramid over 3 months. This is shown by the red curve (Maximum).

During the remaining 9 months there were about 10,000 workers. This is shown by the green curve (Minimum).

There were about 12,400 workers on an annual average. This is shown by the blue curve (Average).

After 15 years, half the height of the pyramid was reached. Since space in the upper area became increasingly limited, fewer and fewer workers could be used.

Therefore, the remaining workers were employed in the quarries in Tura. The blocks of white limestone for the outer casing were obtained there. The orange curve represents the annual average number of workers in Tura. The sum of the orange and blue curves is 12,400 workers, which corresponded to the annual average number of workers for the entire project.

The diagram shows the distribution of the workforce during the 3-month Nile flood.

In the initial phase, the production in the quarries was high. As the pyramid increased in height, the transport routes became longer and, therefore, more and more workers were needed for towing the blocks.

The worker denoted by „Others“ made up almost 40 % of the total number of workers. 25 % were involved in building the ramps and 8 % in preparing food. The proportion of managers and administration was 6 %.

The sum of the curves for Quarries (purple), Towing (blue) and Others (yellow) corresponds to the curve for Total (red).

During the remaining 9 months, the curves were about half as high and the sum of the lower 3 curves corresponded to the green curve in the second to last diagram. This is the corresponding table for the distribution of the workforce.

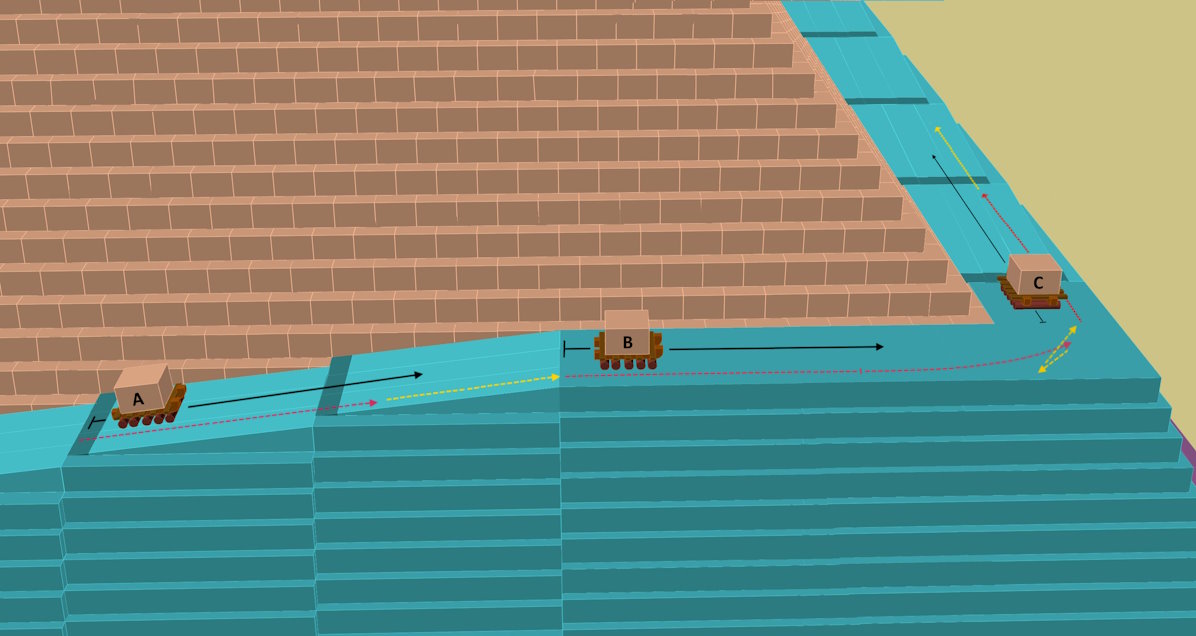
Turning At Corners

The black lines show the length of the respective tow team.

In the first 2.5 minutes, the teams cover the length of the corresponding path marked in red. Team B has to cover twice the length of the path and therefore move at twice the speed. However, this is not a problem because the ramp has no gradient at this point and towing team B therefore only has to pull with a quarter of the force.

Over the next 1.5 minutes, teams will cover the length of the yellow marked path. Team B must first move backwards and then forwards in order to successfully turn at the corner.

Overall, there are no jams and no queuing problems despite turning at the corner. The average speed of the transport process of 3 m/min is guaranteed. This is only possible because the flat portion of the ramp in front of the corner is relatively large.

Huge Blocks

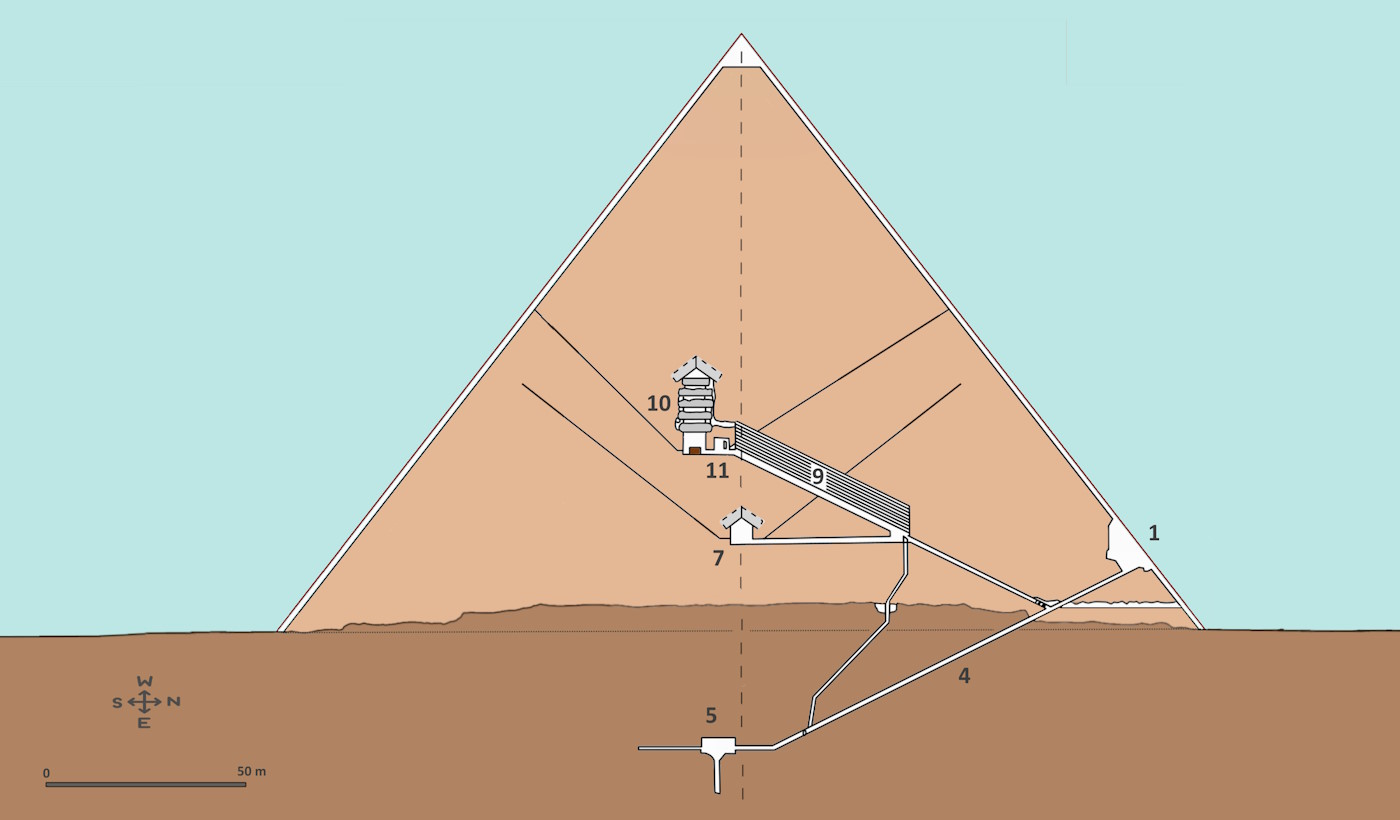
The image shows the north entrance (1).

Blocks of limestone were used for the roof, possibly weighing up to 400 tons.

The precise placement of these blocks was accomplished by controlled lowering with sand and using catch rails.

The same technique was also used to place a 400-ton obelisk on a pedestal. Full details will be presented in a later work (see „Publications“ section).

The image shows a cross section of the Great Pyramid.

Blocks of up to 70 tons were used for the roof of the King’s Chamber (10). Same for the roof of the Queen’s Chamber (7).

More than 100 granite blocks weighing up to 70 tons were used for the Great Gallery (9).

Huge granite stone blocks were used for the sacophagus chamber (11).

To the left of the image are blocks weighing 400 tons. There were a maximum of 12 of these.

To the right there are blocks that weigh 70 tons. There were around 130 of these.

The limestone blocks are shown in yellowish color and the granite blocks in purple color.

The pyramidion was probably placed on the pyramid at an early stage.

In the first 5 years, the huge blocks were brought onto the pyramid using the green ramp. That’s why they didn’t have to be transported on ramps around the corner. This saved the difficult turning at the corners.

The huge blocks were transported upwards from level to level. The temporary brown ramps with a slight slope of 2 degrees were used for this purpose.

The area on the pyramid was always so large that the huge blocks never required more than 15 % of the area.

Pyramidion

In the top third of the pyramid, the green main path is partially positioned on the lower circuit. The path therefore becomes narrower on the lower circuit and only has the capacity of one transport lane.

The pyramidion is 3.3 m wide and weighs 20 tons. Since the area in the upper area of the pyramid is becoming increasingly limited, the pyramidion must be placed on the ramps.

The pyramidion is moved back and forth according to the yellow line. The ramp is increased with a ramp wedge of 2 degrees with each movement. In this way the pyramidion is transported upwards without having to be turned.

The pyramidion is transported on wooden rollers and rolled onto the top platform.

Then the pyramidion is lifted with wedges and the rollers are removed. Using additional wedges it is lowered and placed precisely.

The pointed edge lines in the lower area of the pyramidion were separated. Otherwise the outer edges would break off due to the enormous pressure from the wedges. This is consistent with the historical findings.

The placement of the pyramidion was considered as the completion of the pyramid and the success of the project.

This was celebrated as a topping-out ceremony and a major state act. For this purpose, the Pharaoh and his wife were carried upstairs on the palanquin. The top of the pyramid was packed with all the important people of the state.

On the left is the chief designer Hemiunu, who is celebrated as the hero of the day. The high priest stands in the back and looks jealous.

The wrapping of the ramps created a platform that was covered with a red carpet for the ceremony.

With this transport technology, setting up a pyramidion with a width of 3.3 m and a weight of 20 tons is completely unproblematic.
Even a pyramidion with a base of 4.4 m and a weight of 75 tons could be placed using this construction technique.
From an archaeological point of view, there are no finds of the pyramidion of the Cheops pyramid. It was probably smaller than 2 m at the base and weighed less than 7 tons, as the finds at other pyramids show.

Outer Casing

When the pyramidion was placed, the bottom-up process is completed.

Then the outer casing was installed in a top-down process. At the same time the ramps were removed.

The white limestone was delivered from Tura, 30 km away.

The many ramp paths make it possible to create a work platform on each level at almost any point.

If this is not possible in some places, a work platform can be created using material that was removed further up. This is indicated by the yellow lines.

A direct view to the top of the pyramid is possible at any point. The casing can be sanded with millimeter precision, which results in the high precision of the structure. See the „Precision“ section.

At the end of the top-down process there was a shiny white pyramid in a geometric classic style.

This process only took 0.7 years. Only 0.7 % of material was required based on the pyramid.

The middle edge of each lateral face is shifted slightly inwards. This created greater stability for the casing. See the „Stability“ section.

Magnitude

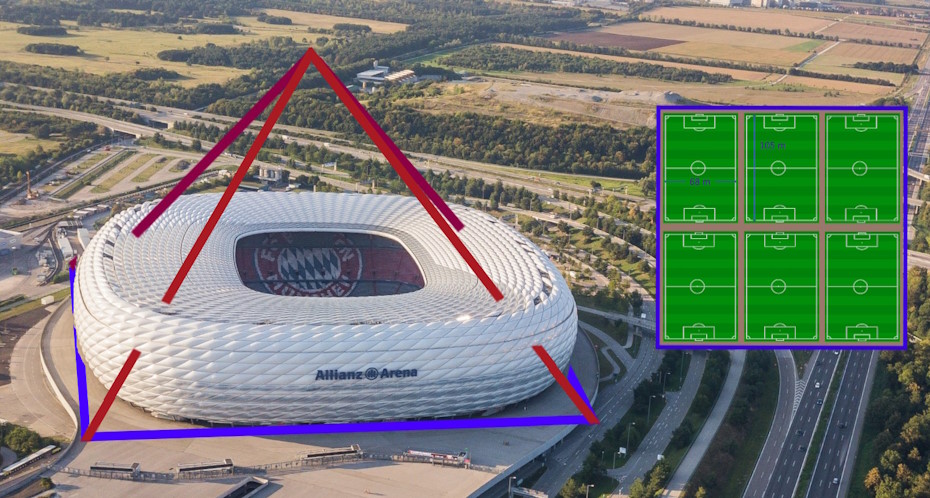
The Great Pyramid is 230 m wide, 146 m high and weighs almost 7 million tons.

The pyramid is so large that the narrow side of the Allianz Arena in Munich would fit in.

The area in the square marked in blue is so large that 6 soccer games could take place there at the same time.

Therefore, it is not surprising that the Great Pyramid was the tallest structure in the world for over 4000 years.

Stability

The Great Pyramid is the only well-preserved of the Seven Wonders of the Ancient World.
It has resisted several serious earthquakes.
One reason for this is the massive bedrock on which it was built.
The casing was very regularly constructed. The same applies to the outer layers of the inner step pyramid. However, the core masonry is irregularly constructed and does not contain any continuous surfaces. This makes it difficult for cracks to propagate.
There are probably rooms filled with gravel, which has a beneficial effect during earthquakes.

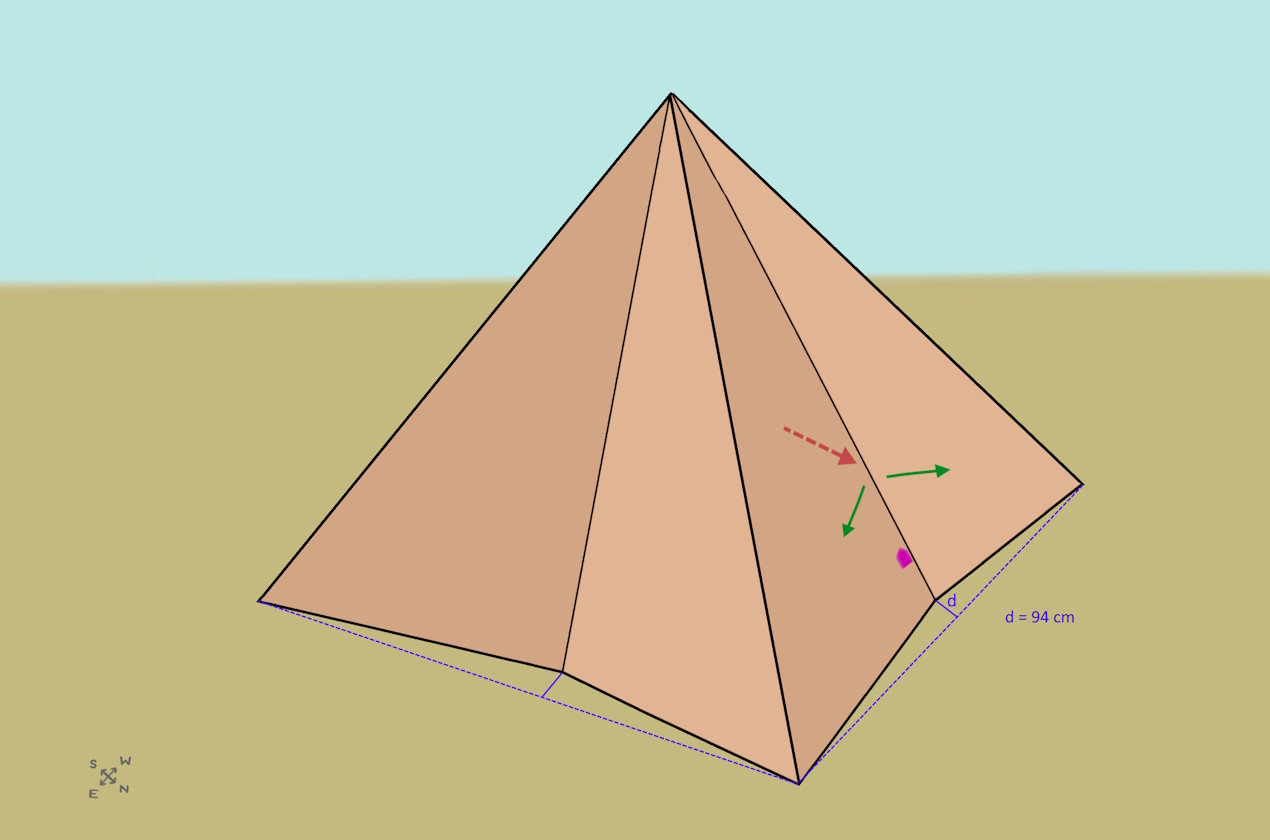
The side surfaces of the pyramid are curved inwards, so the pyramid is 8-sided. On the north side the inward curvature is 94 cm.

The reason for this is the higher stability of the casing. This can easily be seen from the fact that a folded piece of paper is more stable than an unfolded one.

The forces of the red arrow are redirected in the direction of the green arrows. This causes the neighboring stones to become jammed. This prevented the casing from braking out, since this was only slightly anchored to the step pyramid.

The outward pressure is greatest at the central axis. That’s why the north entrance is offset to the east. This is shown in purple.

The outer casing in the upper region actually seems to have been the sensitive region in terms of stability.

The Pyramid of Khafre was built around 40 years later. Its outer casing is not attached in the uppermost region, but rather anchored to the step pyramid. The reason was probably rather against slight shifts due to temperature fluctuations than against damages by earthquakes.

This explains why the part of the outer casing is still there today. The mining was too strenuous even for the stone robbers in the Middle Ages.

This part of the outer casing had to be built from bottom to top along with the step pyramid. At this point, the ramps could not be installed on the step pyramid, but only on the lower circumference. However, this was technically possible.

Diodorus visited Egypt around 60 BC. According to his description, the casing was still in excellent condition, whereas a platform of 3.1 m had formed at the top of the pyramid.

Therefore we can say for sure that the pyramidion was not wider than 3.1 m.

The pyramidion was probably thrown off in the 217 BC earthquake or in an earlier earthquake.

The casing was originally made of white Tura limestone, which was almost completely removed in the Middle Ages.

Measurements And Precision

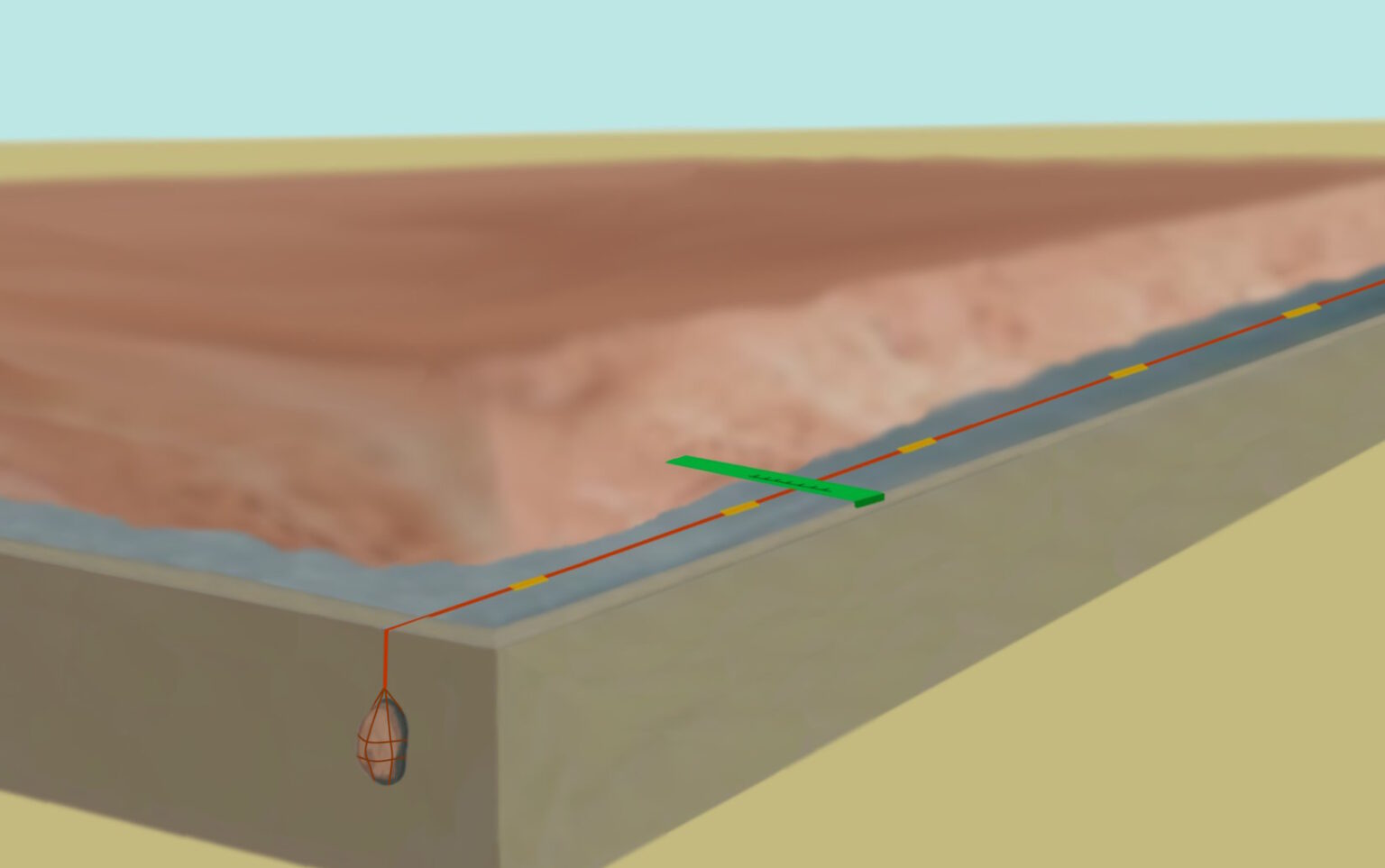
A connected pond has a perfectly planar surface.

To find out if two locations have the same height, can be determined by introducing two identical objects, e.g. stamps or coins.

The leveling or planar creation of a landscape can be done with this measurement technique. A distance of 250 m is no problem.

In the initial phase, the rock core was smoothed and a flat surface was created around it. For this purpose, an artificial pond was built using mud-bricks. Thus a planar surface could be created around the rock core.

A floating cord can be obtained, for example, when uniformly attaching bamboo tubes to a hemp cord. The cord is kept under tension by hanging stones at both ends.

Due to the tension and the mobility in the water, the cord constantly aligns itself or converges into the ideal position.

When taking several measurements at different times with the green measuring scale and then taking the average value, precise values in the millimeter range are obtained over a distance of 250 m.

When building by levels, measurements can be done at any time.

Plane surfaces and straight lines are obtained through artificial water ponds using mud-bricks.

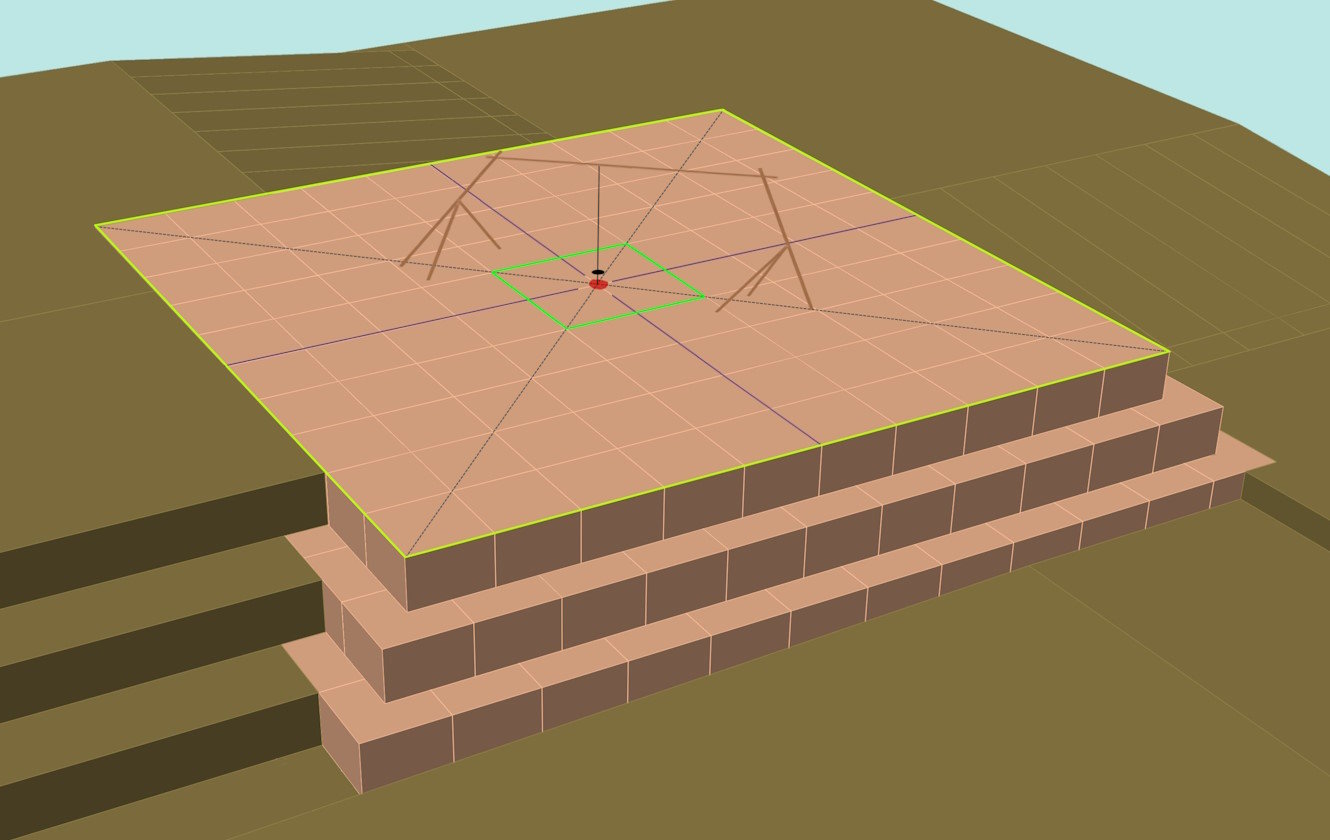
The crucial thing is that the center moves exactly upwards. The best way to do this is to leave a shaft in the middle. This is shown in red color. A plumb is attached on a frame and is hanging down. This can be done in several steps and the individual shaft elements can be filled successively.

To further control the center point, the green square is moved up from one level to the other.

The actual precision work began after the pyramidion was put in place. Then the outer casing was attached.

This was done with millimeter precision. It was possible to look closely at the exterior surfaces from the side and upwards.

It was very important to maintain the angle. For this purpose, a special angle plumb with a length of several meters was made. There was a hanging pendulum on it, which was exactly between the red markings at the intended inclination angle of almost 52 degrees.

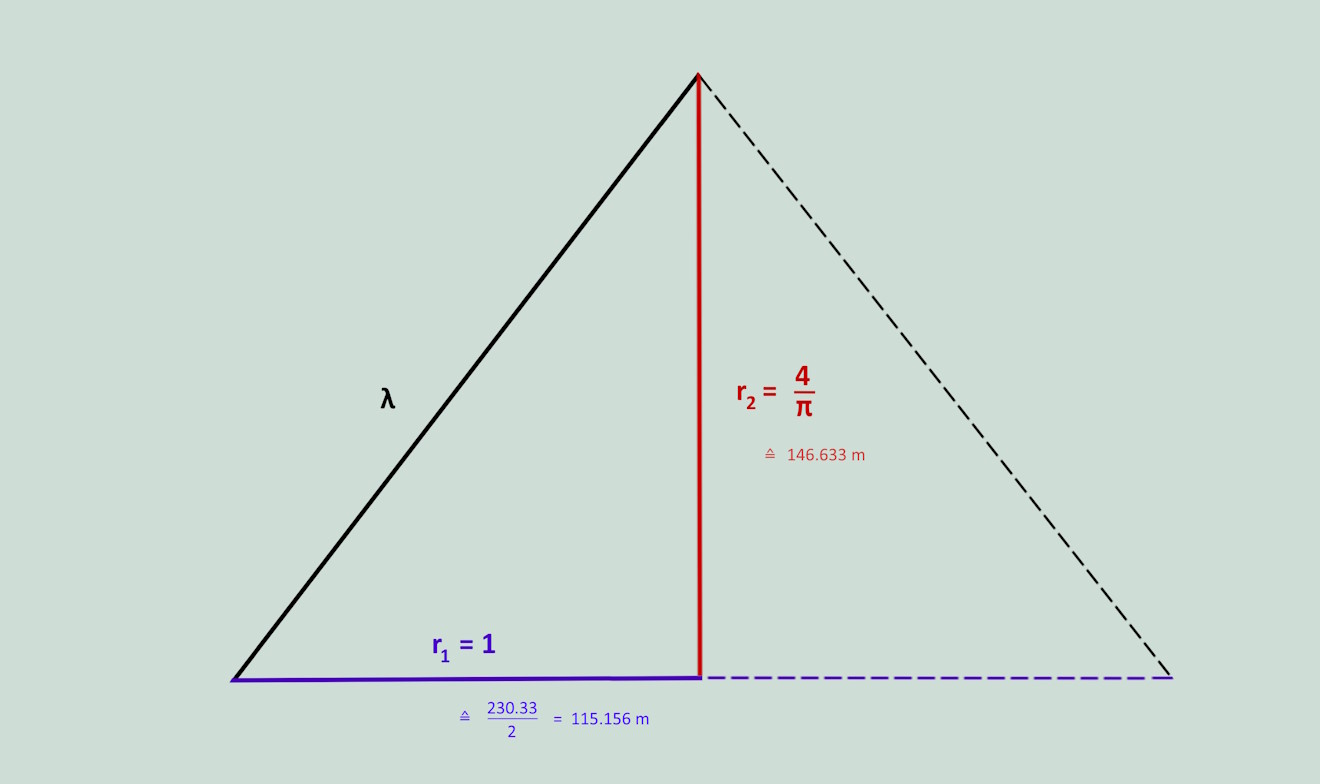
The precise length of the base in the millimeter range was determined late at the end of this process to be 230.33 m.

The planar surface of a pool of water can also be used to grind even surfaces for stone blocks.

Using a granite stone, enough material of a limestone block can be grinded away until it is covered by an even surface of water.

Determining The North-South Direction

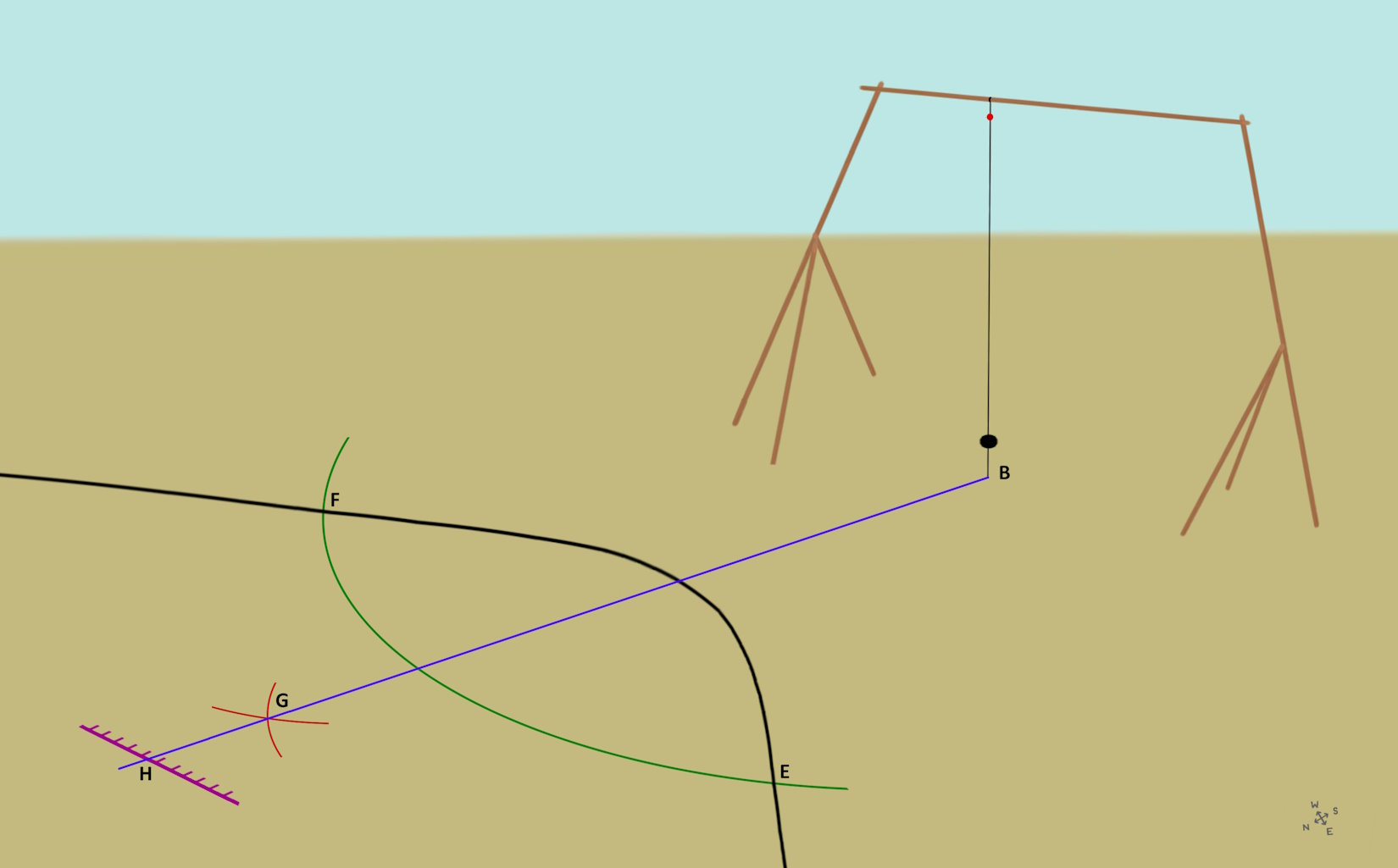
The Cheops pyramid is aligned very precisely according to the four cardinal directions.

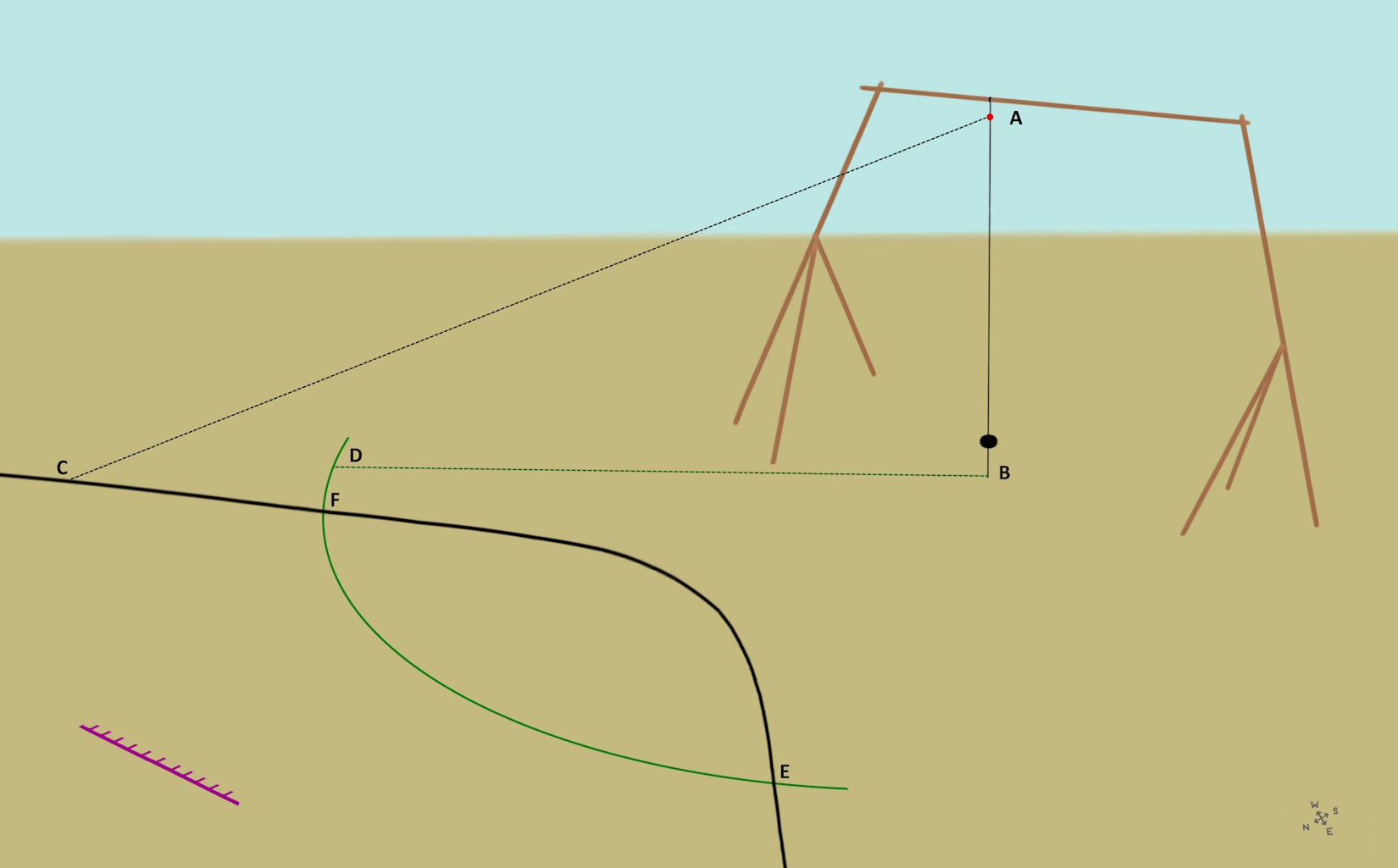
First the north-south direction must be precisely determined. To do this, use an approximately 5 m high plumb as a sundial. This is also known as a shadow pointer or gnomon.

At the lowest point of the gnomon B, the green circle segment with the radius to point D is drawn.

Point A casts a shadow on point C. This can be used to describe the black curve throughout the day. In the winter months the curve bends outwards.

The green and black curves have the two intersection points E and F.

Two red circle segments with the same radius are placed around these two points. These intersect at point G.

Then the blue line is placed through points B and G. This is the north-south direction.

The measuring point H is obtained on the purple measuring scale. Then the experiment is repeated for several days. When taking the average value, very precise values for the north-south direction are obtained.

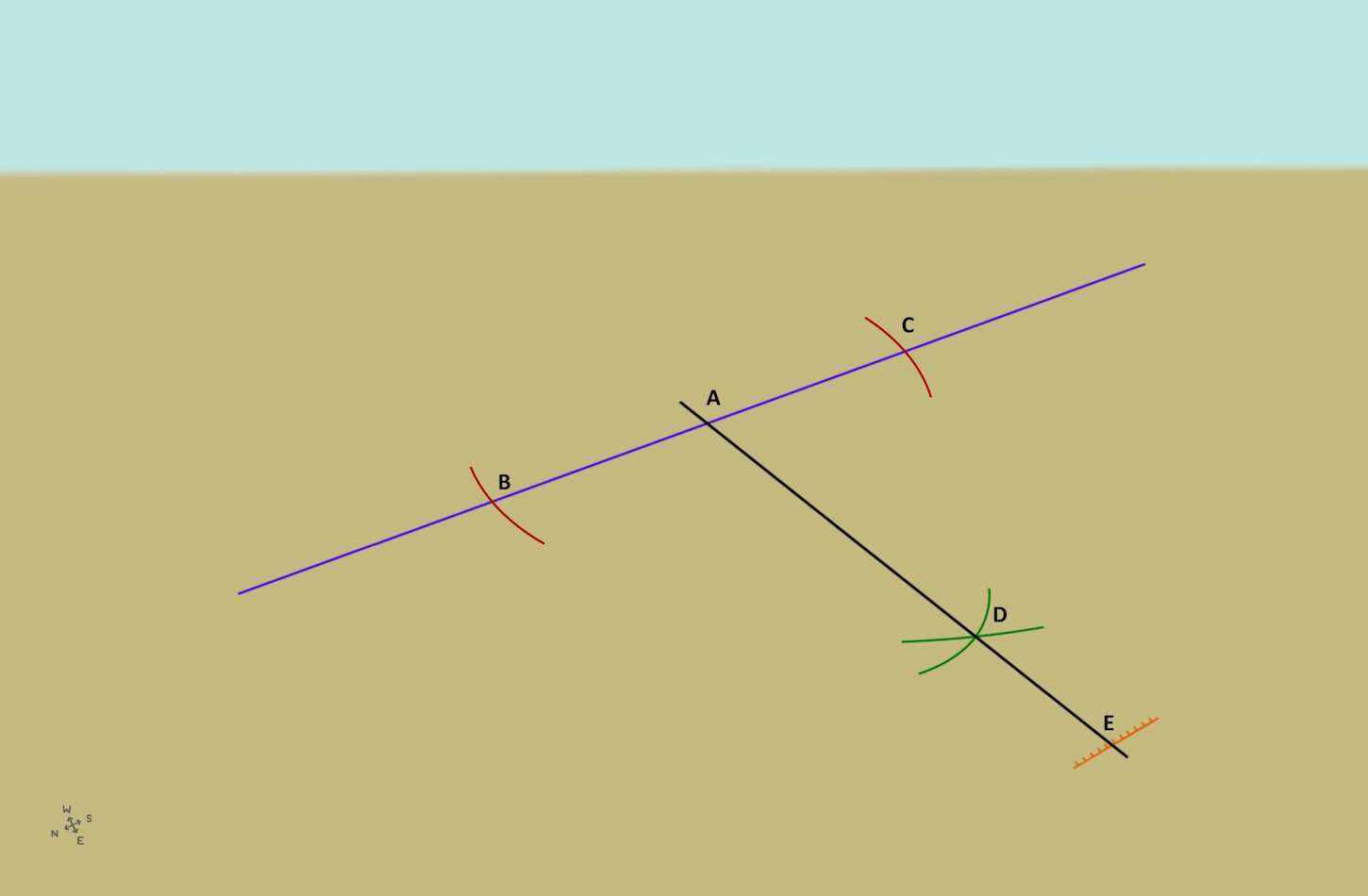
Now a vertical straight line should be generated in the east-west direction. The straight line should go through point A.

A red circle is drawn around the center point A. The circle forms the intersection points B and C with the blue straight line.

Two green circle segments with the same radius are placed around these two points. These intersect at point D. Then the black line is placed through points A and D. This is the east-west direction.

The measuring point E is obtained on the orange measuring scale. When repeating the experiment several times, the east-west direction can be determined very precisely. The Pythagorean theorem is not needed for this elementary method.

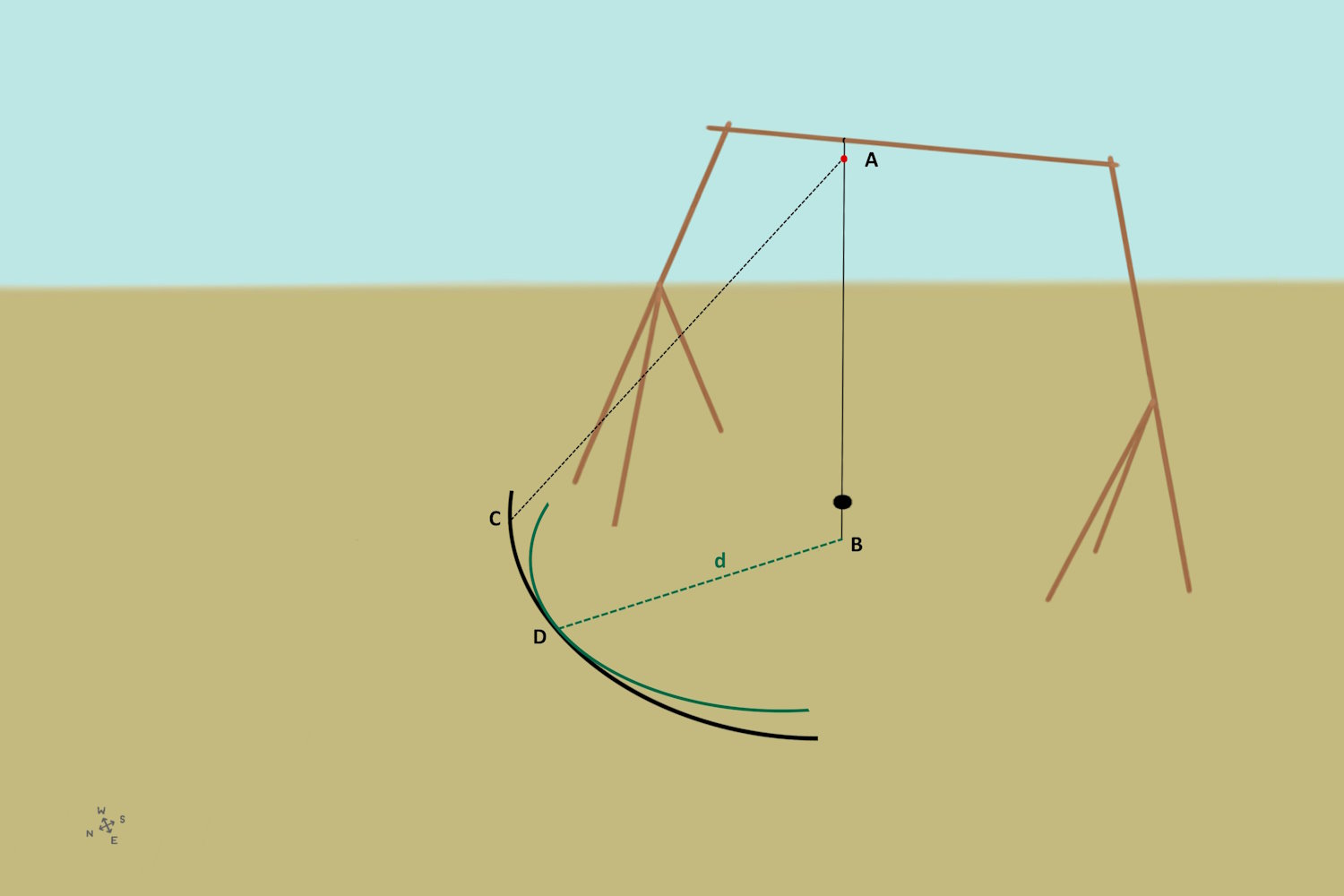
In this context, it should be mentioned that the Earth’s radius can be measured using the sundial method.

The measurement is taken in summer, because the curve is bent inward. The distance d should be as small as possible.

On a certain day of the year in Aswan the distance d=0, i.e. the sun is vertically above the earth at midday.
The same experiment is done on the same day in Alexandria, 835 km away. The radius of the Earth can be calculated based on the deviation of the different values d.

Around 240 B.C. Eratosthenes was able to determine the value with a deviation of less than 5 %. In this respect, it is astonishing that Columbus miscalculated the value by 25 % more than 1,700 years later.

Strategy

The pyramid was much more than just a tomb in memory of the Pharaoh. It was a symbol of power and eternity. It was an early form of what has been called a megamachine since 1970.
That’s why the pyramid was built from the expensive material limestone. The cheap material mudbrick weathers over the centuries, especially when exposed to high levels of moisture. Therefore the motto was:
Stone is for eternity and
mudbrick for the moment.
The Pharaoh was much more than the most powerful man in the state. He was considered a demigod and he was the only one who had the ability to connect with the gods.
After his death, the pharaoh was supposed to ascend to the gods via the pyramid.
From there, he should ensure that all misfortune will be kept away from the state.
Not only he, but all the people in the state should attain eternal life. For this reason, the pyramid can be considered an eternity machine.

Pharaoh Cheops probably came to the throne at a young age. He immediately had to take care of building his pyramid.

The second most powerful man in the state can be seen in the foreground wearing green clothing. He is the vizier and chief designer Hemiunu, a relative of the pharaoh.

He presents a gigantic construction project and presents a pyramidion weighing 20 tons.

The high priest with the fur cloak sees himself in competition with the chief designer and looks suspicious about the matter.

Cheops‘ father, the Pharaoh Sneferu, had a high reputation and a long reign of 50 years.
During this time, Sneferu had built three pyramids, the total volume of which significantly exceeds the Great Pyramid.
Architecturally, they initiate the change from the earlier step pyramids to the real pyramids.
With the Red Pyramid, a real geometric pyramid was planned and completed for the first time right from the start.
Thus, the techniques were developed and tested. The Red Pyramid with a height of 105 m can therefore be viewed as a companion piece to the Great Pyramid.
The chief designer was faced with the challenge of ensuring that Cheops surpassed his father’s reputation through his construction work.
The number of pyramids could no longer be exceeded. The superlative could only lie in the size and perfection of a single one. The motto was:
Not three individuals,
three in one giant.
At the time of planning, Cheops was probably under 20 years old and in excellent health. Therefore, a remaining lifespan of 30 years could be assumed as likely.
The big problem was that the gigantic project would remain unfinished if the Pharaoh died early. The next Pharaoh would not complete the project, perhaps finish it in a three-year construction phase. He might even use the unfinished building as a quarry for his own pyramid. Therefore, the construction prozess was always a fight against time.
Therefore, it was proposed to build the largest pyramid possible in a 30-year project. Several project phases had to be taken into account.

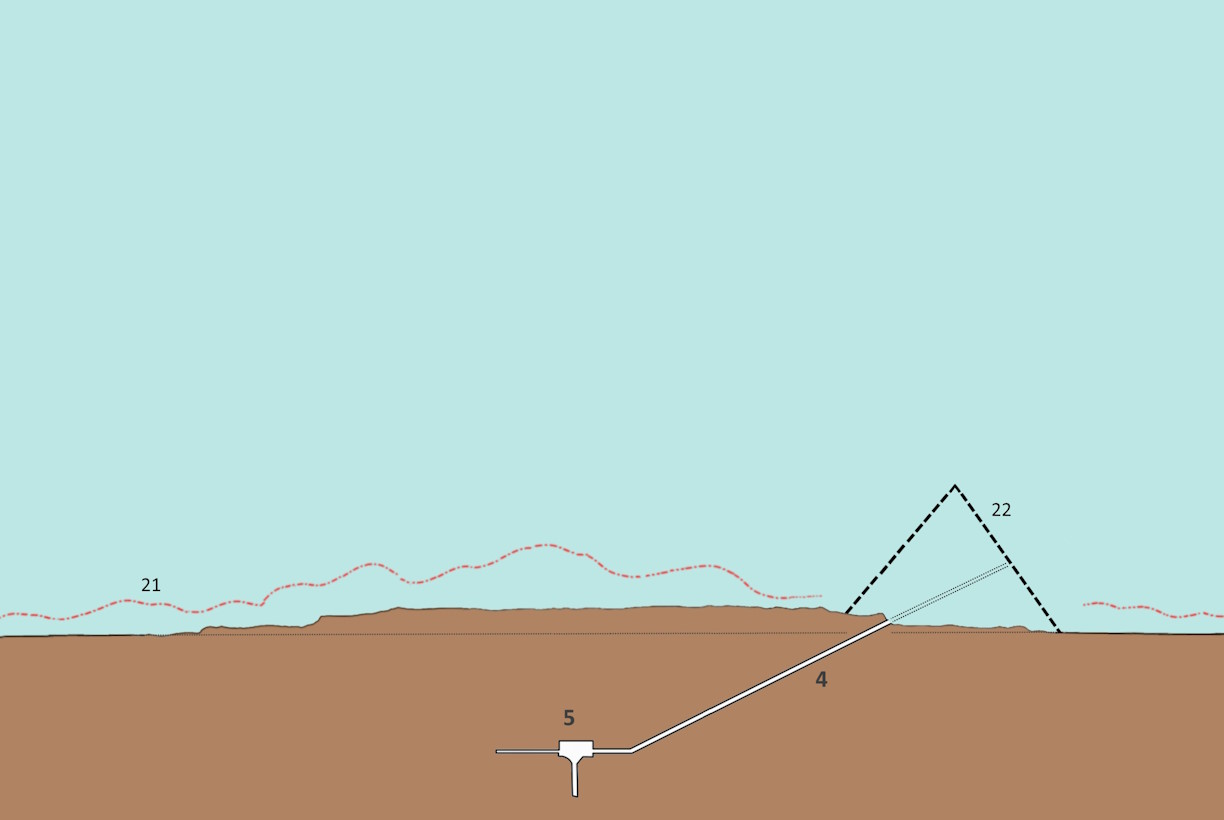
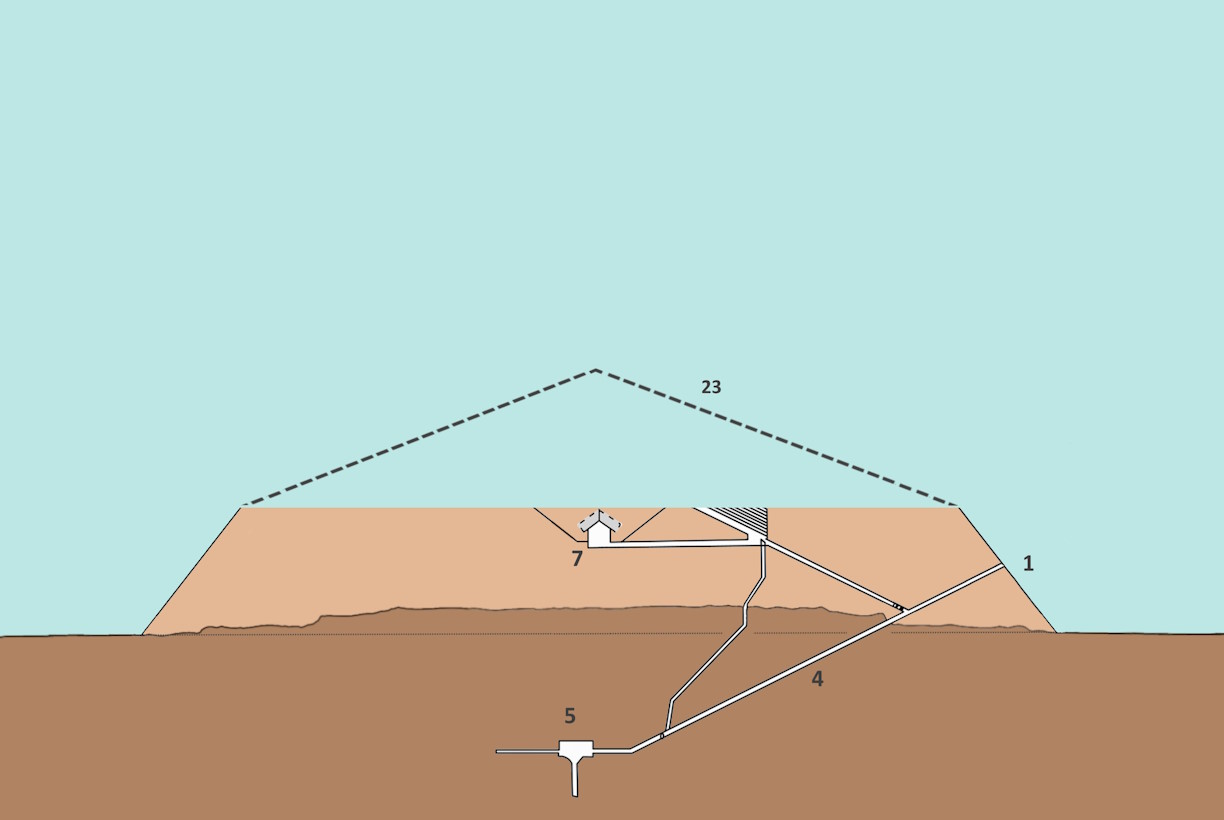
The first project phase lasted 10 years. During this time the workers‘ settlements were built and a large part of the ramp material was produced. Also, the rock core was smoothed. The dashed line shows what the rock core may have looked like before.

The Subterranean Chamber (5) and the Descending Passage (4) were probably carved into the rock very early. If the Pharaoh had died early, there would have been a burial place. In this case, a mini pyramid (22) might have been built at the entrance as an impressive addition.

The construction of the limestone causeway was the main project in this phase. It led from the harbor to the pyramid.

Half of the building material should be used from the 11th to the 17th year.

The Queen’s Chamber (7) was created during this process. This meant that there was a second burial site above ground, which was not yet common at that time. The Subterranean Camber (5) was therefore abandoned.

Thus, at least a mastaba would have existed if the Pharaoh would have died at the end of this construction phase. Perhaps the truncated pyramid would be completed as a bent pyramid (23). Cheops‘ father had one of his pyramids built in this style.

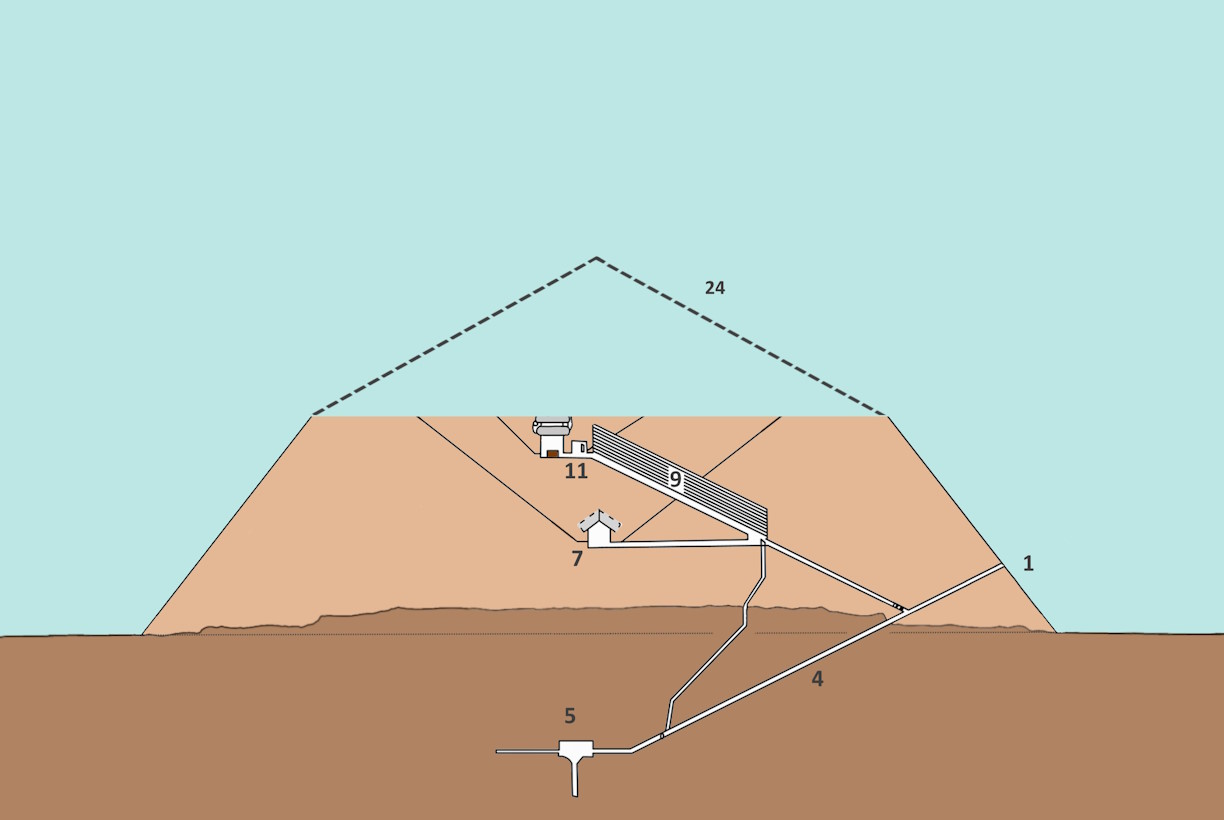
From the 18th to the 21st year, the King’s Chamber (11) was built as the actual burial site. The Grand Gallery (9) was constructed at the same time.

If the Pharaoh would have died at the end of this construction phase, an imposing structure would already be in place if it were completed as a bent pyramid.

The height of the Red Pyramid at 105 m would have already been reached. However, the length of the base of the Red Pyramid at 220 m would be exceeded by 10 m. Thus, Cheops would have surpassed his father not only in the size but also in the precision of construction.

From the 22nd year onwards it was all about completing the pyramid.

The roof of the King’s Chamber (10) was moved high up so that the redirected forces had their effect above the Grand Gallery (9). The forces are shown in blue color.

The inner step pyramid was completed after almost 29 years. During last year, the casing was installed and the ramps were removed.

Cheops‘ reign is said to have lasted at least 30 years. This meant that he was able to surpass his father through his construction project.

According to Herodotus a causeway was built in the first 10 years.

It is said to have been a boulevard that led from the harbor to the pyramid.

The causeway was almost 1 km long, 18 m wide and 14 m high. There are said to have been figures and reliefs on both sides.

When the Pharaoh was carried on the boulevard on a palanquin, he was presented with a colossal picture of figures, a mortuary temple and a pyramid.

Numerology

The circle number π (pi) is defined as the ratio of the circumference and diameter of a circle.

This number is a dimensionless quantity. It is therefore independent of a unit of measurement and independent of culture and time.

A two-dimensional linear stretch can be used to simply justify that this ratio is independent of the size of the circle.

This was already clear to the Egyptians 5,000 years ago, but they were probably not able to calculate the circle number mathematically.

The distinction between a mathematical and a physical constant was probably not made 5,000 years ago. Ultimately it was just a matter of determining the value for structural purposes.

To accurately determine the value, a circle with a radius of approximately 10 m is constructed. Then both the circumference and the diameter are determined using a rolling measuring device. Thus, a measured value for π is obtained.

Multiple measurements are taken and then the arithmetic mean is formed. This compensates for the measurement errors. With hundreds of measurements, the number π can be determined to at least 3 and perhaps even 5 decimal places.

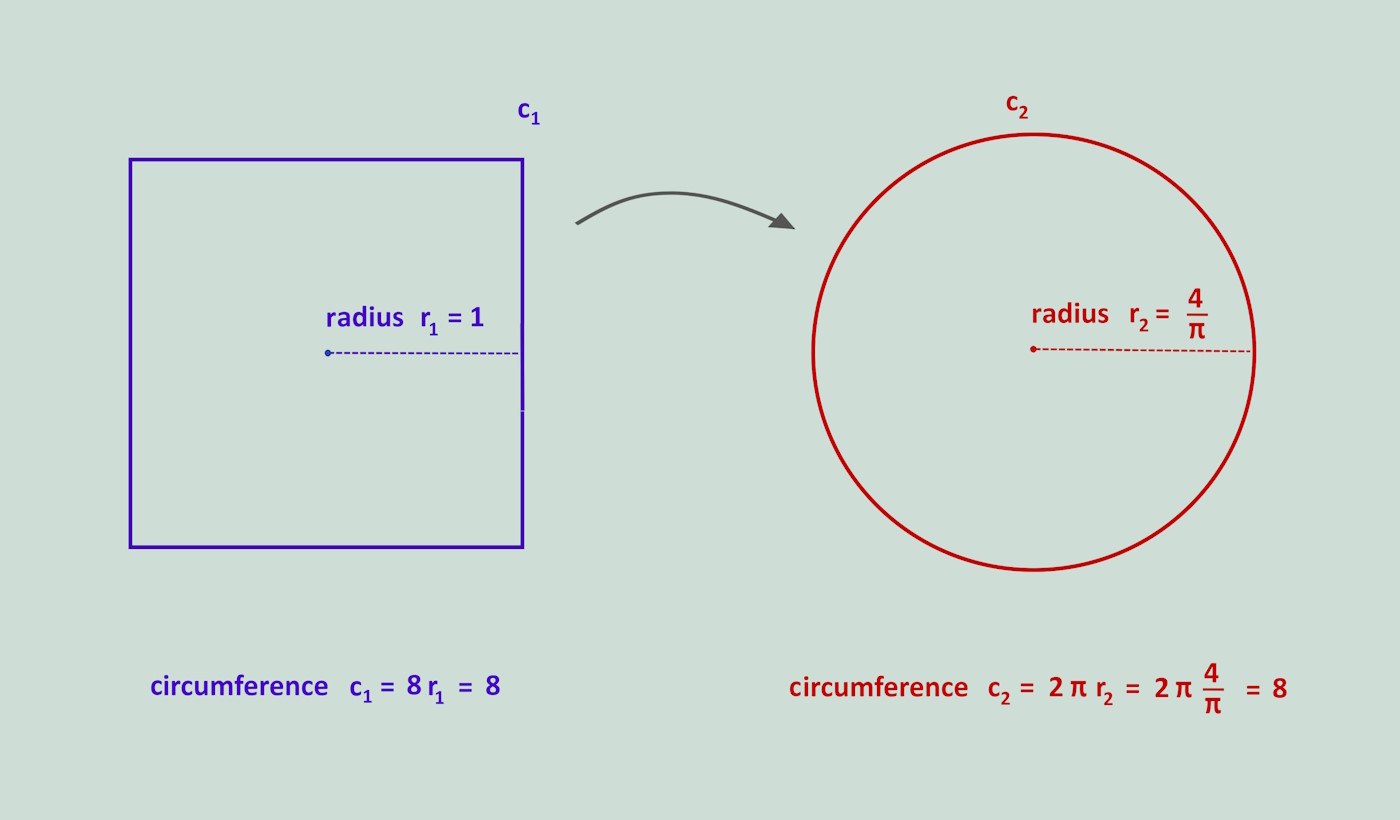
When looking at a square with a diameter of 2 or radius 1, it has a circumference of 8. Now this square should be transformed into a circle so that the circumference is retained. The corresponding circle has a radius of 4/π. This is a kind of inversion of squaring the circle.

The meaning was probably that the square with the number 4 stood for the base of the pyramid and the earthly. The circle, on the other hand, had something eternal due to its rotational symmetry and stood for the sun god Ra or Aton.

The transformation was intended to transform the earthly into the eternal, for which the pyramid was intended as an „eternity machine“.

When looking at the Great Pyramid, it is more than astonishing that half of the base length and the original height are very precisely in the ratio of the two radii.

When taking the value π = 3.142 rounded to 3 decimal places for pi, then the calculated height is 1.362 cm higher than the measured value.

With 4-digit precision or the value π = 3.1416, the calculated height is 3.229 cm too high.

With 5-digit precision or the value π = 3.14159, the calculated height is 3.276 cm too high.

For the sake of simplicity, let’s assume an average height difference of 2.1 cm. This means for 210 levels that the calculated value per level is 0.1 mm too high.

Limestone has water solubility. This can be observed at home at the bottom of the tea kettle and in many other places.

When moisture accumulates between the joints of the blocks, part of the limestone dissolves and then dries between the joints. Therefore, layers of limestone naturally grow together in nature.

This process has probably increased since the Middle Ages due to the loss of the outer casing. Nowadays there might not fit a piece of paper between the crevices, but that was certainly possible 4,500 years ago.

If the pyramid has proportions 1 and 4/π, the Pythagorean theorem can be used to calculate the length of the middle edge λ.

The value λ is very similar to the value ϕ of the golden ratio, but not identical. The same applies to the associated equations. It is most likely that this number had no meaning for the Egyptians 4,500 years ago.

The shape of the pyramid is clearly determined with the proportions 1 and 4/π. The only free parameter is the overall size, which is determined by the base length of 230.33 m. This was probably determined through the maximum size with a construction time of 20 years.

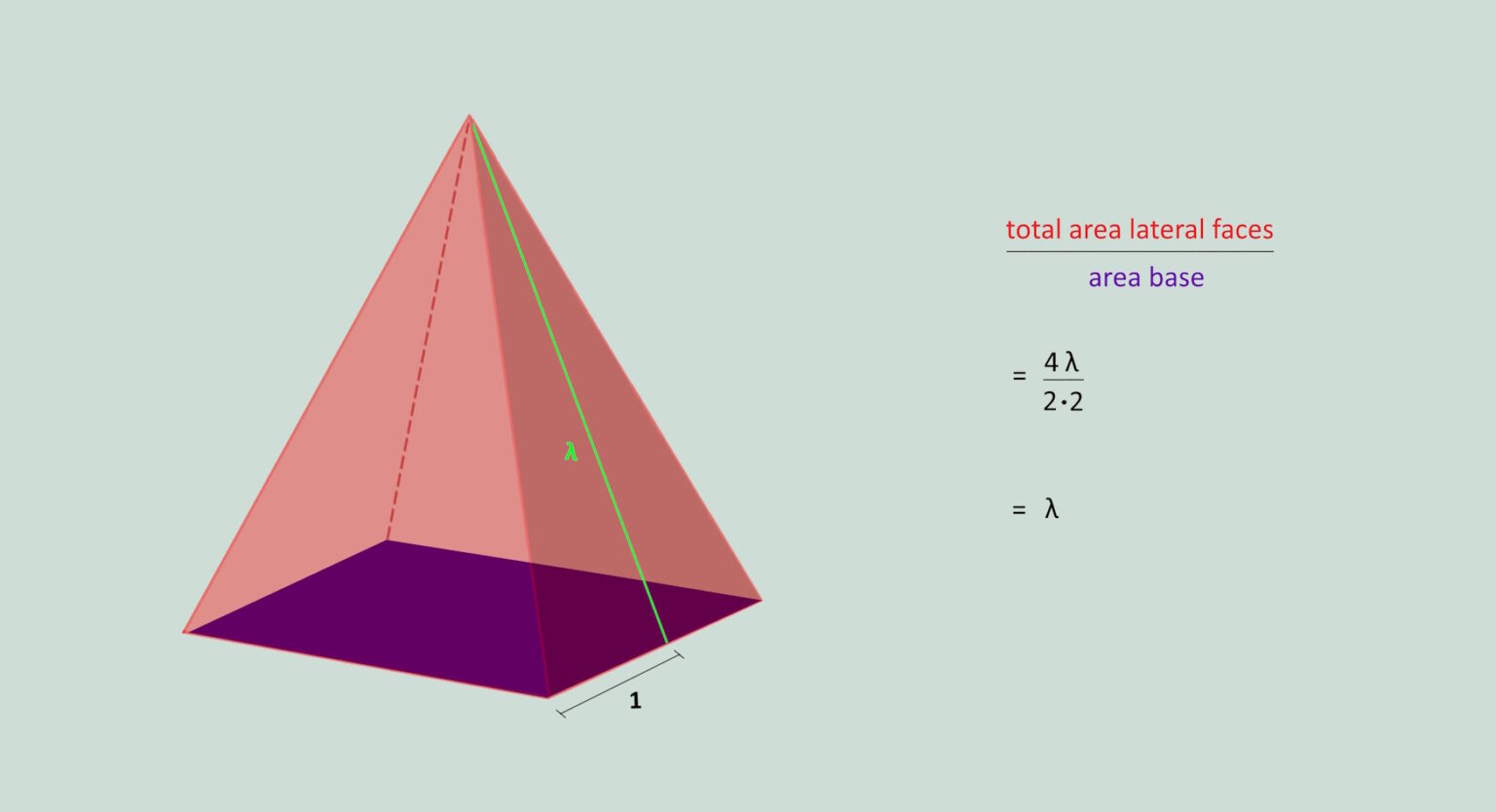
For a pyramid with a base length of 2, the base area has the value 4. This is marked in blue.

If the middle edge has the value λ, then each of the 4 side faces also has the value λ. These are marked in reddish color.

When dividing the 4 side surfaces by the base surface, the value λ results.

This property applies to all square pyramids and is not a special property of the Great Pyramid.

Seven Historical Evidences

The transport technology used corresponds to the description by Diodor that the blocks were transported using ramps and that no lifting devices were used.
The construction method used corresponds to the description by Herodotus that the inner step pyramid was first built and then the outer casing was attached.
The construction was done according to horizontal levels and not according to layers parallel to the outer casing.
The theory explains the construction time of 20 years, which is stated by both Herodotus and Diodorus.
There were 20,000 workers over 3 months during the Nile flood. That was the maximum number of workers working at the same time. This was confirmed by excavations in the workers‘ settlements.
Herodotus describes work assignments of 10 times 10,000 workers, which is usually stated as 100,000 workers. These work assignments are said to have lasted 3 months.
This can probably be interpreted as meaning that during the Nile flood, a total of 10 teams of 10,000 workers each were formed across Egypt. That corresponded to around a third of the farmers at the time. One of the teams had to build the pyramid. Since the maximum number of workers on the pyramid was 20,000, it can be concluded that only 10,000 workers were active in the remaining 9 months.
The model calculates a work performance of 240,000 working years to build the pyramid over 20 years. When adding the first 10 years for the preparation time, the result for the 30-year project is 360,000 working years. This number is given by Diodorus. However, he uses the term „number of workers“ what cannot be true, because this would correspond to about a quarter of the population at the time.

Summary

This hypothesis does not present an unknown technology that has yet to be discovered, as is the case with many other theories. It is simply the efficient application of the two techniques known at the time: spiral ramps and transport with wooden rollers.
The method solves the problem one hundred percent technically and logistically, so there are no unanswered questions in this regard.
Furthermore, the method is consistent with the previous „Seven Historical Evidences“. So far, there are no contradictions due to historical or archaeological findings.
This hypothesis is the first functional solution. Therefore, the construction method no longer has to be considered an unsolved mystery of mankind.

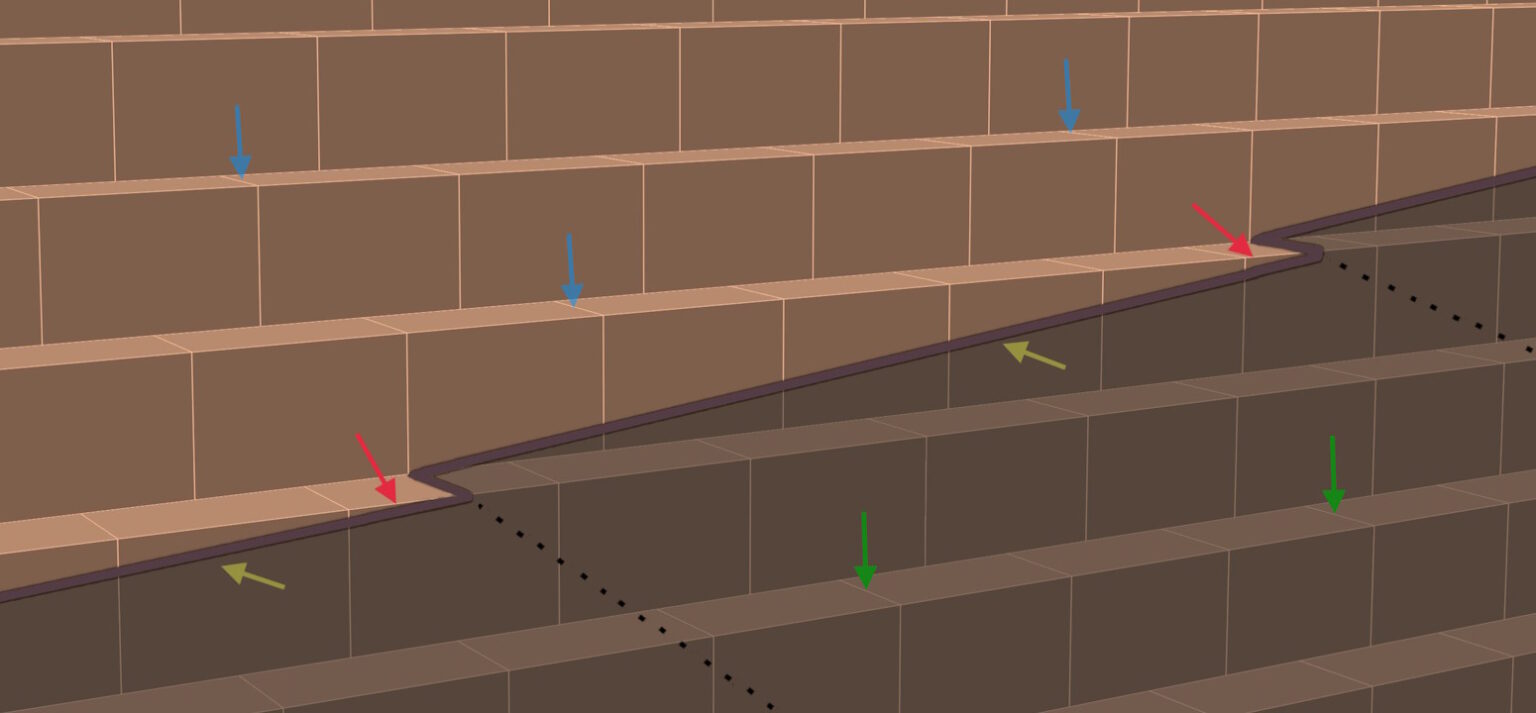
Archaeological Finds

Archaeologists generally do not believe in pure hypotheses. Only relevant finds are important for them.
There is very little hope that the construction method will ever be revealed by papyrus finds or grave inscriptions. The archaeologist Dieter Arnold stated this already in 1981: „It is no longer possible to determine how the Egyptian builders managed their work. However, the examples of the Cheops and Chephren pyramids demonstrate that they succeeded in solving the problem“.
Therefore, the question arises whether this hypothesis will forever remain a semi-archaeological solution that cannot be further verified due to the lack of finds. Or can further findings be gained in the future that support or deny this hypothesis?

Suppose the pyramid had actually been built according to the present theory. What possible archaeological traces would the ramps have left on or between the blocks? Can this be used to check the course of the ramps?

The ramps were probably the largest in the lowest part of the south side and were in place throughout the entire construction period. That’s why the traces should be clearest there.

There may be discolorations on the outside surfaces of the blocks where the ramps were placed. This could have been caused by the ramps directly or, for example, by leaking oil in the supply area. The corresponding locations are marked by yellow arrows.
There could be discolorations, especially in the areas where the toilets were. There should be traces of urine stone in the blocks.
Geologist Prof. James Harrel Prof. James Harrel believes that there must be varying concentrations of dried brick residue between the crevices of the stones. In places where there were ramps, the concentration would have to be significantly higher than in places where there were no ramps. The corresponding locations are marked by green and blue arrows.
He also assumes that there should be abrasions and marks of wear at the beginning of the individual ramp wedges. The corresponding locations are marked by red arrows.
When conducting the investigations, it must be taken into account that the outer casing was installed with the utmost precision during the top-down process. It is therefore possible that the outermost layer of the inner step pyramid was readjusted in some places.
It must also be taken into account that during the top-down process, ramp material was temporarily installed at each location. Overall, there were only temporal differences for the individual locations in how long the ramp material was installed there, e.g. 10 years or just one month.

Publications

There is the newspaper report Mystery of History Solved from the Mitteldeutsche Zeitung.

The corresponding scientific work is entitled Constructing The Cheops Pyramid Through Multispiral Ramps and will be published on October 17, 2024 in the Journal of Humanistic Mathematics of the Claremont Colleges in California. That’s exactly three years since the project began. The work comprises 140 pages including 50 pages of calculation tables.
The introduction can already be downloaded.

The technology for the precise positioning of the 400-ton blocks will be published in a separate work. This topic is closely related to the erection of a 400-ton obelisk, what is the second unsolved enigma. The work is entitled Setting Up An Egyptian Obelisk and will be published on October 17, 2025.

The idea, proof finding and implementation were developed by Dr. Rudolf Volz. He is a qualified mathematician, has developed software for many years and is interested in the central problems of humanity.

The three-dimensional CAD models were created by Rudolf Höld using the moi3d software.

This work was supported by Keyoo, individual keyboards for computers and games.

Sources: Image 1 and the background of Image 3 are courtesy of Mosaik Education.
Images 2, 7, 8, 12 use elements from 123rf.com.
Image 4 is by Gouchet, image 5 is by Peter Jackson and image 6 is by Dows Dunham.
Image 12 is from the film „First View of this Pyramid Construction Technique“ on YouTube.
Images 7, 13.14 use elements from Q-Files. Image 8 is from Alamy.
Images 9, 16, 17, 18, 19 use elements from Cleanpng.
Image 20 uses elements from Alamy and Cleanpng.
All other images are copyright of Dr. Rudolf Volz.

Imprint (2023 – 2024) – Deutsche Mediengesellschaft mbH – Auf den Steinen 2 – D-06485 Quedlinburg, Germany – info@cheops-pyramid.net